på 2024-06-20 328

Opnå spidsydelse med den maksimale effektoverførselsteorem

Princippet om den maksimale effektoverførselsteorem er et fundament inden for elektroteknik, der understøtter effektivt kredsløbsdesign og optimal strømforsyning på tværs af forskellige anvendelser fra industriel til forbrugerelektronik.Dette teorem teoretiserer, at for en kilde med en endelig intern modstand leveres maksimal effekt til belastningen, når belastningsmodstanden er nøjagtigt lig med kildens interne modstand.Denne artikel graver sig i en mangefacetteret udforskning af dette teorem, der undersøger dens teoretiske underbygninger gennem linsen af ​​Thevenins teorem og dens praktiske konsekvenser i forskellige applikationer, der spænder fra DC -kredsløb til komplekse vekselstrømssystemer.Ved at dissekere den matematiske formulering og anvende beregning til at udlede betingelser for maksimal kraftoverførsel, præciserer artiklen ikke kun de teoretiske aspekter, men broer også kløften til applikationer i den virkelige verden.Det gennemgår afvekslingen mellem maksimal effektoverførsel og effektivitet, især relevant i energisensitive applikationer, og udvider diskussionen til den strategiske anvendelse af impedans, der matcher til at forbedre systemets ydelse i lydsystemer, effektelektronik og telekommunikation.

Katalog

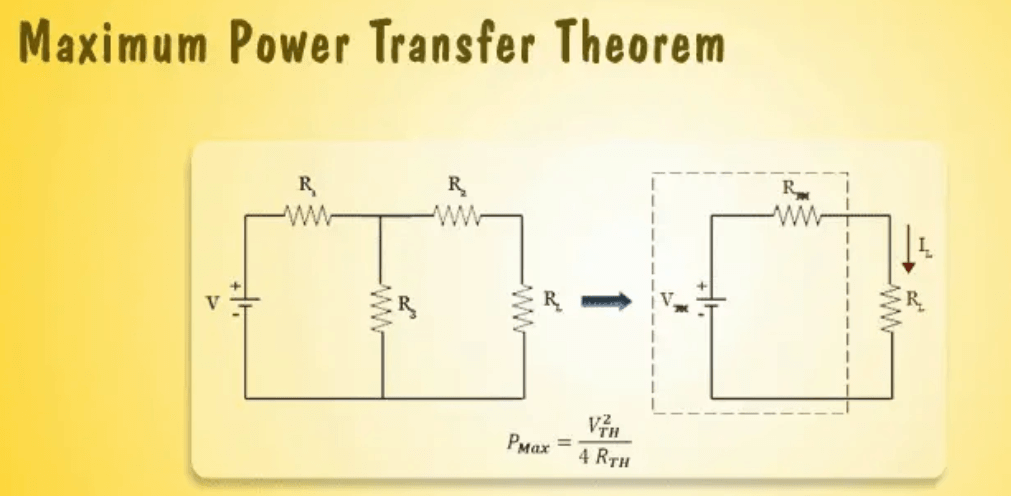
Figur 1: Maksimal teorem for kraftoverførsel

Værdier for den maksimale effektoverførselsteorem

Den maksimale effektoverførselsteorem er nøglen til DC -kredsløbsdesign og effektoptimering.Det hedder, at for at maksimere strømoverførslen fra en kilde til en belastning, skal belastningsmodstanden svare til kildens interne modstand.Denne betingelse sikrer optimal strømforsyning.

Ved hjælp af Thevenins sætning kan et DC -strømforsyningssystem modelleres som en spændingskilde i serie med en modstand.Denne model forenkler beregninger af strømoverførsel.I henhold til Ohms lov, magtS er givet afS=jeg²R hvor jeger aktuel og Rer modstand.Strømmen, der leveres til belastningen, maksimeres, når belastningsmodstandenR_L Matcher kildemodstandenR_S.På dette tidspunkt er spændingen over belastningen halvdelen af ​​kildespændingen og optimerer den leverede strøm.

At opnå maksimal kraftoverførsel involverer finjustering af belastningsmodstanden for at matche kildens interne modstand.Dette gøres gennem iterative justeringer og målinger.For eksempel kan et kredsløbsdiagram med Thevenins ækvivalent og en belastningsmodstand illustrere virkningen af ​​modstandsjusteringer på effektoverførselseffektiviteten.

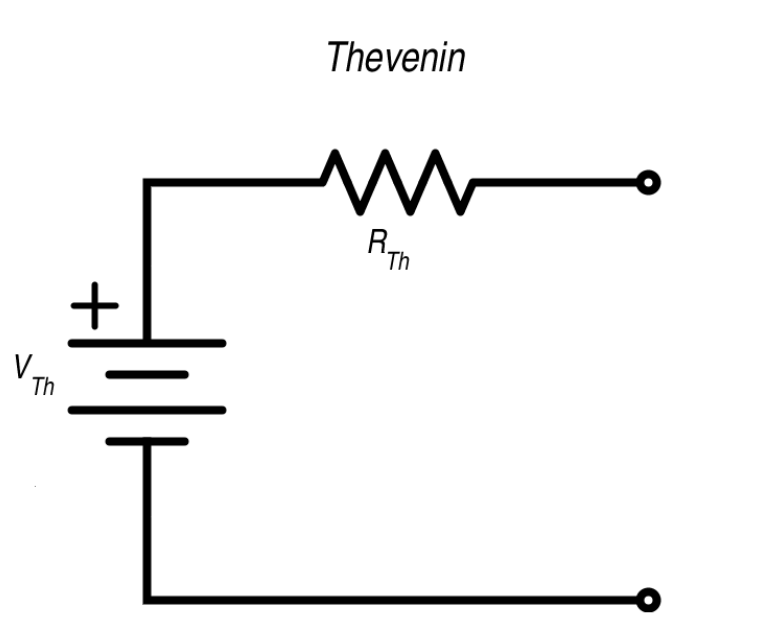
Figur 2: Illustrerende eksempel på maksimal kraftoverførsel

Eksempel på maksimal strømoverførsel

For at forstå den praktiske anvendelse af den maksimale strømoverførselsteorem, lad os undersøge et Thevenin -ækvivalent kredsløb.Indstil Thevenin -modstanden ved 0,8 ohm.For optimal kraftoverførsel skal belastningsmodstanden også være 0,8 ohm.Under disse forhold opnår kredsløbet en effekt på cirka 39,2 watt.

Overvej nu, hvad der sker, når du ændrer belastningsmodstanden.Hvis du justerer det til 0,5 ohm eller 1,1 ohm, ændres strømafledningen markant.Ved 0,5 ohm ser kredsløbet en stigning i strøm, men lavere effektivitet på grund af et højere spændingsfald over den interne modstand.Ved 1,1 ohm falder den nuværende strømning, hvilket fører til lavere effektafledning.Dette viser, at effekten kun maksimeres, når belastningsmodstanden matcher kildemodstanden.

Sætningen er ikke kun teoretisk;Det er dynamisk i design af effektive kraftsystemer.For eksempel maksimerer transmitterens outputimpedans med antennens impedans i radiosenderdesign med radiospedansen signalstyrke og rækkevidde.I solenergisystemer skal gitterbundne invertere matche inverterens outputimpedans med gitterets impedans for at optimere strømoverførsel, hvilket forbedrer effektiviteten og pålideligheden af ​​solinstallationer.

Forståelse af afvekslingen: Maksimal effekt vs. maksimal effektivitet

Den maksimale effektoverførselsteorem skelner mellem maksimering af effektoverførsel og opnåelse af maksimal effektivitet, især i AC -kraftsystemer.I AC -strømfordeling er målet at forbedre effektiviteten, hvilket kræver en lavere generatorimpedans sammenlignet med belastningsimpedansen.Denne tilgang er forskellig fra teoremets retningslinje, der rådgiver matchende impedanser for optimal strømoverførsel.

Figur 3: Lydsystemer

I lydsystemer med høj tro er det vigtigt at opretholde en lav outputimpedans på forstærkere i forhold til en højere højttalerbelastningsimpedans.Denne opsætning minimerer strømtab og bevarer lydkvaliteten og viser en afvigelse fra teoremets anbefaling om maksimal strømoverførsel.

Figur 4: RF -forstærkere

For RF -forstærkere, hvor lav støj er risikabelt, bruger ingeniører ofte impedansovertrædelse.Denne strategi reducerer støjinterferensen i modsætning til teoremets forslag.Den maksimale effektoverførselsteorem fokuserer på at maksimere effekten, men overvejer ikke effektivitet eller støj, som er mere nødvendige i disse scenarier.

Afsløring af formlen for maksimal strømoverførsel

Grundlaget for den maksimale strømoverførselssætning er et simpelt matematisk udtryk, der forbinder udgangseffekten på tværs af en belastning (S_L） Til DC -kildeegenskaber og belastningens modstand (R_L） Formlen er:

Her, V_Th er thevenin ækvivalent spænding ogR_Th er den ækvivalente modstanden for kilden.Denne formel er påkrævet for at identificere de optimale betingelser for strømoverførsel.

For at finde betingelserne for maksimal strømoverførsel bruger vi beregning.Ved at indstille derivatet af strømligningen For nul ser vi, at maksimal strømoverførsel sker, når belastningsmodstanden R_L er lig med thevenin -modstanden R_Th .Dette sikrer, at spændingen på tværs af belastningen er halvdelen af ​​kildespændingen, hvilket fører til den mest effektive strømafgivelse i den givne kredsløbskonfiguration.

Denne teoretiske ramme er nøglen til både akademiske studier og praktiske anvendelser.Det giver en klar retningslinje for ingeniører, der designer kredsløb, hvor effektiv kraftoverførsel er et must.

Detaljeret bevis og analyse af den maksimale effektoverførselsteorem

Det er det ultimative eksempel på at bruge beregning i elektroteknik.Processen starter med at konvertere ethvert kredsløb til dets theveninækvivalent.Dette forenkler kredsløbet til en enkelt spændingskilde (V_Th) og en seriemodstand (R_Th).

Sætningen siger, at strømmen spredte sig over belastningsmodstanden (R_L） Maksimeres under specifikke betingelser.Vi begynder med at oprette strømafledningsformel:

For at bestemme betingelsen for maksimal effekt, tager vi derivatet af S_LvedrørendeR_L og indstil det til nul:

Ved at løse denne ligning gennem differentiering og algebraisk forenkling finder vi detR_L=R_Th er poenget med maksimal strømoverførsel.Dette betyder, at belastningsmodstanden, der maksimerer kraftoverførsel, er lig med kildens thevenin -modstand.Yderligere verifikation, såsom anden derivatforsøg eller planlægning af funktionen, bekræfter det vedR_L=R_Th Strømafledning når sit højdepunkt.

Evaluering af effektivitet i maksimale strømoverførselsscenarier

Den maksimale effektoverførselsteorem hjælper med at optimere strømoverførslen, men dens effektivitet er begrænset til 50%.Denne effektivitet kommer fra forholdet mellem den strøm, der leveres til belastningen til den samlede effekt af kilden.Når belastningsmodstanden (R_L） Svarer til thevenin -modstanden R_Th Begge modstande forbruger lige strøm, hvilket opdeler kildeneffekten lige mellem belastningen og den interne modstand.

For at beregne dette skal du overveje den samlede effekt leveret af kilden:

Når R_L=R_Th , kraften på tværs R_Ler:

Således effektiviteten Som forholdet mellem kraften på tværs af belastningen og den samlede effekt er:

Dette afslører en betydelig kompromis inden for systemdesign.Optimering for maksimal strømoverførsel betyder ofte at ofre effektivitet.

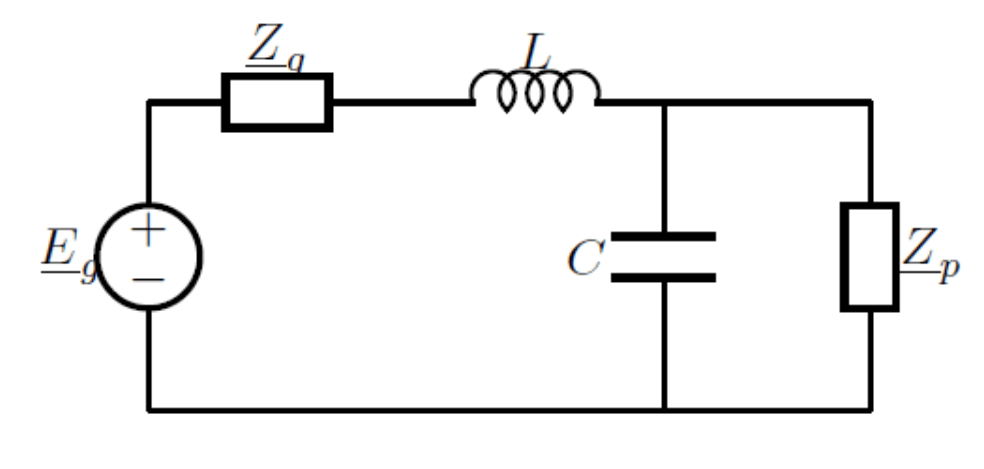
Figur 5: Impedans, der matcher i forstærkerkredsløb

Optimering af impedans, der matcher for overlegen kraftoverførsel

Impedans -matching, en teknik fra den maksimale effektoverførselssætning, bosætter sig i outputstadierne af forstærkerkredsløb.Denne proces involverer justering af impedansen hos højttalere til at matche forstærkerens outputimpedans ved hjælp af matchende transformere.Denne justering optimerer forstærkerens evne til at overføre maksimal strøm til højttalerne, hvilket forbedrer den samlede lydudgang.Ved at matche impedans fungerer forstærkeren under sine mest effektive kraftoverførselsbetingelser.Dette maksimerer lydudgangen og bevarer lydfidenskab ved at minimere tab, der opstår, når impedanser er uoverensstemmende.Disse tab forekommer ofte som varme eller reflekteret kraft, som kan forringe ydelsen og potentielt skade forstærkeren eller højttalerne.

I praksis involverer implementering af impedans matchning at vælge transformere, der kan håndtere forstærkerens effektvurdering og give det korrekte transformationsforhold, der matcher højttalerens impedans.Dette sikrer, at energien fra forstærkeren effektivt omdannes til lyd energi snarere end spildt.Derfor forbedres kvaliteten og volumenet af lydudgangen.

Figur 6: Maksimal effektoverførselssætning for DC- og AC -kredsløb

Anvendelse af den maksimale strømoverførselssætning i AC- og DC -kredsløb

Den maksimale effektoverførselsteorem er et ultimativt princip inden for elektroteknik, der gælder både DC- og AC -kredsløb, skønt dens implementering varierer mellem de to.

For DC -kredsløb siger sætningen, at maksimal effektoverførsel opstår, når belastningsmodstanden er lig med kildemodstanden.Denne justering er alvorlig til at designe effektive kraftsystemer og er især betydningsfuldt i batteridrevne enheder og solenergisystemer.I solcellepanelesystemer justerer effektoptimerne for eksempel belastningens effektive modstand mod at matche solcellernes optimale outputresistens og derved maksimere energioverførsel og forbedre systemets effektivitet.Denne tilgang forbedrer ikke kun effektiviteten, men udvider også levetiden for energikilden ved at minimere effekttab.

I AC -kredsløb er anvendelsen af ​​sætningen mere kompleks på grund af tilstedeværelsen af ​​fasevinkler og reaktive komponenter.Maksimal effektoverførsel i vekselstrømskredsløb opstår, når belastningsimpedansen er det komplekse konjugat af kildeimpedansen.Dette involverer justering af belastningens reaktive komponent til at være ens og modsat af kilden, hvilket effektivt annullerer reaktive elementer og justerer fasevinkler.Dette princip anvendes i systemer, hvor faseforvrængning kan påvirke ydelsen alvorligt, såsom RF -sendere og lydforstærkere.Resistive og reaktive komponenter skal beregnes omhyggeligt og afbalanceres inden brug, typisk kondensatorer og induktorer, for at justere fasen og derved maksimere effekten og forbedre systemets kvalitet og pålidelighed.

Anvendelser af den maksimale effektoverførselsteorem

Den maksimale effektoverførselsteorem spiller en alvorlig rolle i forbedring af effektivitet og ydeevne på tværs af forskellige teknologier, især på elektroniske enheder, solcellepanelesystemer og lydsystemer, hvor der er behov for optimal impedansmatching.

Figur 7: Elektroniske enheder

I elektroniske enheder sikrer sætningen, at effektforstærkere leverer maksimal effekt til belastningen.I trådløse kommunikationssystemer matcher ingeniører for eksempel omhyggeligt impedansen af ​​senderen til antennens antenne for at minimere effekttab og maksimere signaleffektiviteten.Under praktiske operationer bruger ingeniører netværksanalysatorer til at måle og justere impedans, finjustering af komponenter som induktorer og kondensatorer for at opnå den ønskede kamp.Disse justeringer påvirker den samlede ydelse, der fremhæver teoremets betydning i applikationer i den virkelige verden.

Figur 8: Solpanelsystemer

I solcellepanelesystemer optimerer den maksimale effektoverførselssætning energi -konvertering.Kraftproduktionen fra et solcellepanel afhænger af belastningsimpedansen, der er præsenteret af inverteren eller opladningskontrolleren.Ingeniører bruger maksimal Power Point Tracking (MPPT) algoritmer til dynamisk at justere belastningsimpedansen til at matche panelets interne impedans, hvilket sikrer maksimal effektekstraktion under forskellige sollysforhold.Dette involverer kontinuerlige overvågnings- og realtidsjusteringer, der kræver sofistikerede softwarealgoritmer og dataanalyse.Ved at redegøre for subtile variationer i sollys og temperatur er denne proces både kompleks og nøgle til at maksimere effektiviteten.

Figur 9: Lydsystemer

I lydsystemer er korrekt impedansmatching dynamisk for lydudgang af høj kvalitet.Lydingeniører bruger sætningen til at matche impedansen hos højttalere med forstærkere, sikre maksimal kraftoverførsel og minimere forvrængning for klar lyd.Under opsætningen anvender ingeniører værktøjer som impedansbroer og lydanalysatorer til at finjustere systemet.Denne nøjagtige matching involverer ofte justering af crossover -netværk og valg af passende højttalerkabler, hvilket demonstrerer vigtigheden af ​​detaljer for at opnå overlegen lydkvalitet.

Implikationer af den maksimale effektoverførselsteorem

Den maksimale effektoverførselssætning giver bemærkelsesværdige fordele, såsom forbedret strømforsyning og reduceret komponentstress, hvilket fører til sikrere og mere effektive kredsløbsdesign.Imidlertid har det også begrænsninger, herunder en 50% effektivitetshætte og uanvendelighed til ikke-lineære systemer.

Sætningen sikrer, at belastningen får maksimal effekt fra kilden, når belastningsimpedansen matcher kildenimpedansen. Praktisk set involverer dette ingeniører, der bruger impedans-matchende teknikker under kredsløbsdesign.For at illustrere netværksanalysatorer og impedansbroer i RF -kredsløbsdesign måler og justerer impedansen af ​​forskellige komponenter, hvilket sikrer optimal strømforsyning.Denne nøjagtige matching minimerer strømtab og bosætter sig i højfrekvente applikationer, hvor selv små uoverensstemmelser kan føre til betydelige ineffektiviteter.

Ved at sikre maksimal kraftoverførsel reducerer sætningen stress på komponenter. Matchende impedanser afbalancerer aktuelle og spændingsniveauer, hvilket forhindrer overdreven varme og potentiel skade på kredsløbselementer.Ingeniører bruger termisk billeddannelse og aktuelle sonder til at overvåge komponentpræstation under belastning.Justeringer til køleplade og kølesystemer er ofte påkrævet for at opretholde optimale betingelser, hvilket forbedrer kredsløbets levetid og pålidelighed.

Nedsat komponentstress bidrager til sikrere kredsløbsdesign. I effektelektronik forhindrer korrekt impedans matchning overophedning og elektriske fejl.Ingeniører udfører detaljerede simuleringer og stresstest for at sikre, at komponenter fungerer inden for sikre grænser.Dette involverer modellering af kredsløbets termiske og elektriske opførsel ved hjælp af softwareværktøjer, efterfulgt af fysisk test for at validere modellerne.Denne iterative proces sikrer, at det endelige design er både effektivt og sikkert.

På trods af sine fordele har sætningen begrænsninger. En større begrænsning er 50% effektivitetshætten, hvilket betyder, at kun halvdelen af ​​den strøm, der leveres af kilden, når belastningen, mens Den anden halvdel spredes i kildenimpedansen.Dette er især relevant i batteridrevne og energi-høstapplikationer, hvor effektiviteten er utrygt.Ingeniører skal afbalancere behovet for maksimal kraftoverførsel med de samlede effektivitetskrav, og vælger ofte design, der afviger lidt fra sætningen for at opnå højere effektivitet.

Sætningen gælder ikke for ikke-lineære systemer, hvor forholdet mellem spænding og strøm ikke er proportional.I praktiske scenarier, såsom skifte strømforsyninger og digitale kredsløb, er ikke-lineære komponenter som transistorer og dioder almindelige.Ingeniører bruger alternative teknikker, såsom load-line-analyse og små-signalmodellering, for at optimere strømoverførsel i disse systemer.Disse metoder involverer detaljeret karakterisering af komponenternes ikke-lineære opførsel og specialiserede simuleringsværktøjer til at forudsige og forbedre ydeevnen.

Løsning af netværksproblemer ved hjælp af den maksimale effektoverførselsteorem

Implementering af den maksimale effektoverførselsteorem i netværksanalyse involverer en systematisk tilgang.Dette inkluderer identifikation af belastningsmodstanden, beregning af Thevenin -modstanden og spænding og anvendelse af sætningen for at bestemme optimale kraftoverførselsbetingelser.

Identificer først belastningsmodstanden (R_belastning) I kredsløbet.Dette involverer at undersøge kredsløbsskemaet og bruge værktøjer som ohmmetre eller impedansanalysatorer til at måle belastningskomponentens modstand.Præcis måling er nøglen, da selv mindre unøjagtigheder kan påvirke den samlede analyse.Ingeniører skal kalibrere måleværktøjer og overveje temperaturkoefficienten for resistive materialer til præcision.

Beregn derefter den ækvivalente modstand R_Th og spænding V_Th:

Open-kredsløbsspænding (V_Th ): Mål eller beregne spændingen over belastningsterminalerne med belastningen fjernet.Brug et voltmeter med høj impedans for at undgå at indlæse kredsløbet og fordreje målingen.

Thevenin modstand (R_Th ): Bestem den ækvivalente modstand set fra belastningsterminalerne med alle uafhængige spændingskilder erstattet af kortslutninger og uafhængige strømkilder med åbne kredsløb.Ingeniører bruger ofte simuleringssoftware som Spice til at modellere kredsløbet og beregnes nøjagtigt thevenin -modstanden.Overvej parasitiske elementer og komponenttolerancer i dette trin.

Med R_Th og V_Th Bestemt, anvende sætningen for at sikre maksimal effektoverførsel ved at matche belastningsmodstanden mod thevenin -modstanden:

Juster belastningsmodstanden for at matche R_Th.Dette kan involvere valg af en belastningsmodstand med den nærmeste mulige værdi eller ved hjælp af en variabel modstand (potentiometer) til finjustering.Overvåg den strøm, der leveres til belastningen ved hjælp af strømmålere og termiske sensorer for at sikre sikker og optimal drift.

Efter indledende justeringer skal du kontrollere ydelsen.Brug oscilloskoper og spektrumanalysatorer til at kontrollere spændings-, strøm- og power -bølgeformer.Finjustering kan være påkrævet for at redegøre for ikke-idealiteter i den virkelige verden, såsom kontaktbestandighed og temperaturvariationer.

Figur 10: Transmissionslinieovervejelser

Transmissionslinjeydelse med den maksimale effektoverførselsteorem

I systemer, der involverer transmissionslinjer (såsom koaksiale kabler og snoede parkabler), er nøjagtig impedans, der matcher ved kilden og belastningsender.Ingeniører anvender tidsdomæne -reflektometri (TDR) til at måle og visualisere disse refleksioner ved at injicere et testsignal og analysere de reflekterede signaler for at identificere misforhold og foretage nødvendige justeringer.

Karakterisering af transmissionslinjen

Brug en netværksanalysator til at måle den karakteristiske impedans af transmissionslinjen.Dette værktøj sender en række frekvenser gennem linjen og måler de reflekterede signaler for at bestemme impedansen.

Kalibrer netværksanalysatoren ved hjælp af kendte standarder for at sikre nøjagtige målinger, der kompenserer for eventuelle iboende fejl i målesystemet.

Matchende kildenimpedansen: Juster kildeimpedansen for at matche transmissionslinjens karakteristiske impedans.Dette kan involvere tilføjelse af matchende netværk, såsom serie- eller parallelle modstande, kondensatorer eller induktorer.Brug et oscilloskop til at verificere kildesignalintegriteten.Se efter en ren bølgeform uden forvrængninger, hvilket indikerer minimale refleksioner.

Matchende belastningsimpedans: Juster belastningsimpedansen for at matche transmissionslinjens karakteristiske impedans.Dette kan involvere finjustering af belastningen ved hjælp af variable komponenter eller design af tilpassede impedans-matchende netværk.Mål signalet ved belastningsenden ved hjælp af et oscilloskop og netværksanalysator for at sikre, at bølgeformen forbliver uforvrækket, hvilket bekræfter en vellykket impedans matchning.

Højhastigheds- og analoge signalkontekster: I højhastigheds digitale kredsløb og analoge signalapplikationer eskalerer alvorligheden af ​​impedans, der matcher, med højere frekvenser, hvor spørgsmål som krydstale, elektromagnetisk interferens (EMI) og dæmpning bliver mere udtalt.Ingeniører tackle disse udfordringer gennem omhyggelig design og test, hvilket sikrer, at transmissionslinjer dirigeres med kontrolleret impedans ved hjælp af PCB -designsoftware udstyret med integrerede impedansregnemaskiner til design af spor med den korrekte bredde og afstand.De implementerer korrekt jordforbindelse og afskærmningsteknikker, såsom jordplaner, afskærmningsindkapslinger og differentiel signalering, for at minimere EMI.Derudover designer ingeniørfiltre til at afbøde uønskede frekvenser og støj ved hjælp af filterdesignsoftware og kredsløbssimulatorer og implementere signalkonditioneringskredsløb som forstærkere og dæmpere for at opretholde signalkvalitet over lange afstande.Finjustering af disse kredsløb sikrer, at de matcher impedans- og frekvensegenskaberne for transmissionslinjen.

Subtile operationelle overvejelser: Temperatureffekter kan forårsage, at transmissionslinjekarakteristika varierer, hvilket kræver brug af temperaturkompenserende materialer og design til at opretholde en ensartet impedansmatchning.Endvidere har komponenter i den virkelige verden tolerancer, der kan påvirke impedansmatchning;Således er det nødvendigt at vælge højpræcisionskomponenter og udføre toleranceanalyse i designfasen for at afbøde disse problemer.I systemer, der oplever dynamiske belastningsbetingelser, er implementering af adaptive impedans matchningsteknikker, såsom elektronisk indstillelige matchende netværk, nøglen til at opretholde optimal ydelse.

Konklusion

Den maksimale effektoverførselssætning fungerer som en nødvendig ramme til optimering af strømforsyning i elektriske kredsløb, hvilket afbalancerer vanskelighederne i teoretiske elektriske principper med de praktiske krav fra moderne ingeniørapplikationer.Selvom den tilvejebringer en metode til at maksimere effekten, introducerer den også en risikabel overvejelse af effektiviteten, især relevant i dagens energibevidste miljø.Den detaljerede undersøgelse af teoremets applikationer - fra solcellepanelesystemer til sofistikerede lydopsætninger - underscores dens alsidighed og nyttige rolle i at forbedre ydelsen og pålideligheden af ​​teknologiske systemer.Ikke desto mindre fremmer den iboende effektivitetshætte og dens begrænsede anvendelighed til ikke-lineære systemer en nuanceret applikation, der opfordrer ingeniører til at undertiden afvige fra teoremet for at prioritere den samlede systemeffektivitet frem for blot effektmaksimering.Således beriger dette teorem ikke kun vores forståelse af elektrisk kredsløbsadfærd, men guider også tekniske beslutninger i et landskab, hvor effekteffektivitet og systemoptimering er dominerende.

Ofte stillede spørgsmål [FAQ]

1. Hvad er den maksimale effektoverførselsteorem og Nortons sætning?

Maksimal effektoverførselsteorem: Dette princip siger, at for at opnå maksimal ekstern effekt fra en kilde med en endelig intern modstand, skal belastningenes modstand svarende til kildens modstand.

Nortons sætning: Dette sætning forenkler et netværk til en enkelt strømkilde og parallel modstand.Det siger, at ethvert to-terminalt lineært kredsløb kan erstattes af et tilsvarende kredsløb bestående af en Norton-strømkilde parallelt med en Norton-modstand.

2. Hvad er det maksimale teoremkompleks for effektoverførsel?

Når det kaldes "komplekse", betyder det normalt at anvende sætningen i kredsløb, hvor komponenterne, inklusive kilder og belastninger, har kompleks impedans snarere end rent modstandsdygtige elementer.Betingelsen for maksimal effektoverførsel i denne sammenhæng er, at belastningsimpedansen skal være det komplekse konjugat af kildeimpedansen.

3. Hvad er det maksimale effektprincip?

Dette er et andet udtryk, der ofte bruges ombytteligt med den maksimale effektoverførselssætning.Det henviser til retningslinjen for at optimere effekten ved at justere belastningen, der matcher kildens interne modstand eller impedans.

4. Hvad er trinnene i den maksimale strømoverførselssætning?

Identificer kildemodstanden: Bestem den interne modstand for kilden eller den thevenin -modstand set fra belastningen.

Beregn eller juster belastningsmodstand: Indstil belastningsmodstanden lig med kildens interne modstand.

Kontroller eller ansøg: I praktiske scenarier kan dette involvere justering af en variabel modstand eller beregning af den forventede belastning for at sikre, at den matcher kildemodstanden for maksimal effektivitet.

5. Hvad er fordelen ved den maksimale strømoverførselsteorem?

Den primære fordel er dens evne til at optimere effektiviteten af ​​strømforsyning fra en kilde til en belastning, især nyttig i kommunikation (som at maksimere signalstyrken på tværs af en antenne) og andre elektroniske anvendelser, hvor effekteffektivitet er alvorlig.Imidlertid kommer dette ofte på bekostning af øget energitab i selve kilden, hvilket måske ikke altid er ønskeligt i magtfølsomme applikationer.