Anvendelse af Ohms lov i seriekredsløb
Elektriske kredsløb, hvad enten de er enkle eller komplekse, styres af grundlæggende love, der forudsiger deres opførsel under forskellige forhold.Et seriekredsløb, der er kendetegnet ved en enkelt kontinuerlig sti, gennem hvilken strømmen strømmer, giver et klart eksempel på disse principper i handling.For effektivt og sikkert at udvikle, evaluere og fejlsøge elektriske systemer er det påkrævet at forstå, hvordan strømmen opfører sig i et sådant kredsløb, at artiklen graver i kompleksiteten i seriekredsløb, understreger ensartethedens ensartethed, anvendelsen af Ohms lov ogdistribution af modstand.Gennem praktiske eksempler og detaljerede beregninger undersøger det den operationelle dynamik i seriekredsløb, udforsker både enkelt- og flere modstandskonfigurationer og udvider disse koncepter til analyse af parallelle kredsløb.Udforskningen begynder med en forståelse af strømmen i et seriekredsløb, sammenlignet med marmor, der bevæger sig ensartet gennem et rør og udvides til at omfatte omfattende anvendelser af Ohms lov til at bestemme kredsløbsadfærd.Denne grundlæggende forståelse baner vejen for yderligere diskussioner om mere komplekse konfigurationer og deres implikationer i den virkelige verden elektriske applikationer.Katalog
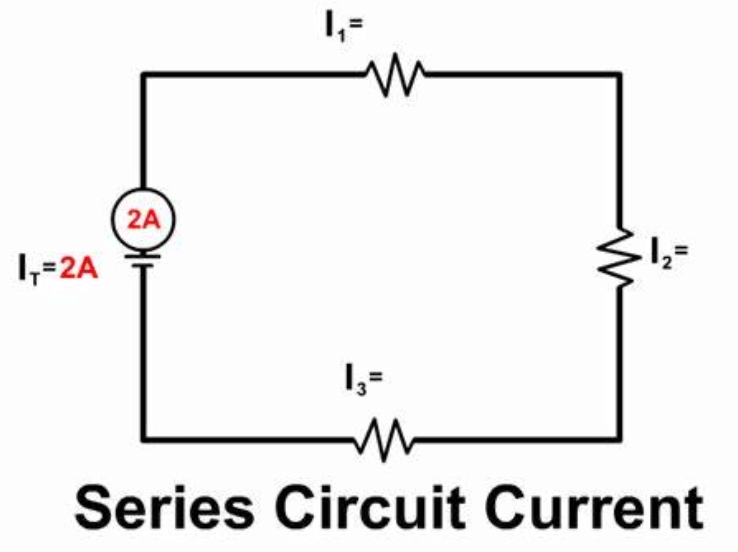
Figur 1: Seriekredsløb
Nuværende dynamik i seriekredsløb
I et seriekredsløb strømmer den elektriske strøm gennem en enkelt, kontinuerlig sti, hvilket sikrer, at den samme strøm passerer gennem hver komponent.Tilsvarende opretholder vand, der strømmer gennem en uforgrenet slange, en ensartet hastighed.Dette illustrerer, hvorfor hver komponent i en serie kredsløb oplever den samme strøm.
For effektivt at analysere og forudsige, hvordan et seriekreds opfører sig under forskellige forhold, er det dominerende at bruge Ohms lov.Denne lov forklarer forbindelsen mellem spænding, strøm, modstand og strøm i et kredsløb.Når du anvender Ohms lov, skal du måle spænding, strøm og modstand mellem de samme to punkter.Dette sikrer, at dine beregninger af spændingsfald og strømstrømme er nøjagtige og afspejler de faktiske forhold i kredsløbet.

Figur 2: Ohms lov i kredsløb
Implementering af Ohms lov i kredsløb med en enkelt modstand
Når man undersøger et grundlæggende seriekredsløb, der inkluderer en enkelt modstand og et batteri, er det nødvendigt at forstå, hvordan komponenterne er tilsluttet.Punkter i kredsløbet, der er forbundet med ledere med minimal resistens, betragtes som elektrisk identiske.For eksempel markerer punkter 1 og 4 i et kredsløb med et 9V -batteri og en modstand, at 1 og 4 markerer terminalerne på henholdsvis batteriet og modstanden.Spændingen over modstanden, mellem punkter 2 og 3, er 9V.Denne opsætning demonstrerer Kirchhoffs spændingslovgivning, der siger, at summen af alle spændinger omkring enhver lukket kredsløbssløjfe skal svare til nul.
Brug af Ohms lov, repræsenteret af ligningen Vi kan nemt beregne den aktuelle strømning gennem modstanden.Her,jeg er aktuel, Ver spændingen og R er modstanden.For at anvende dette i vores eksempel overvejer vi spændingen over modstanden (punkter 2 og 3) og modstandsværdien.
Vi kan nemt beregne den aktuelle strømning gennem modstanden.Her,jeg er aktuel, Ver spændingen og R er modstanden.For at anvende dette i vores eksempel overvejer vi spændingen over modstanden (punkter 2 og 3) og modstandsværdien.
Eksempel beregning
Antag, at modstanden er 3 kΩ.Den nuværende, der flyder gennem modstanden, beregnes som følger:

Denne beregning tilvejebringer et direkte mål for strøm baseret på kendt spænding og modstandsværdier.Det giver ingeniører mulighed for nøjagtigt at identificere og løse problemer relateret til spændingsfald og aktuelle fordelinger inden for kredsløbet.Anvendelse af OHMs lov på denne måde forbedrer pålideligheden og effektiviteten af det elektriske systemdiagnostik og vedligeholdelse, hvilket sikrer nøjagtig og effektiv problemløsning.
Ohm's Law in Action: Seriekredsløb med flere modstande
Når man beskæftiger sig med seriekredsløb, der inkluderer flere modstande, kræver anvendelse af OHMs lov en mere detaljeret tilgang på grund af den måde, hvorpå spænding distribueres over hver modstand.Den samlede spænding fra batteriet (f.eks. 9V mellem punkter 1 og 4) forbliver konstant, men spændingsfaldet over hver modstand varierer baseret på deres modstand.Dette skyldes, at den samlede spænding er delt mellem modstandene i forhold til deres modstandsværdier.
Beregning af total modstand
Først skal du beregne kredsløbets samlede modstand ved at opsummere modstandsværdierne for alle modstande i serie.For eksempel, hvis du har tre modstande R1, R2og R3, den samlede modstand RTotal er givet af:RTotal=R1+R2+R3
Bestemmelse af den samlede strøm
Når den samlede modstand er kendt, skal du bruge Ohms lov til at finde den samlede strøm, der flyder gennem kredsløbet:
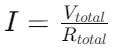
Eksempel beregning
Antag, at R1 er 2 kΩ, R2 er 3 kΩ, og R3 er 5 kΩ.Den samlede modstand RTotal ville være:

Ved hjælp af et 9V -batteri er den samlede nuværende III:

I et seriekredsløb strømmer den samme strøm gennem alle komponenter.For at finde spændingsfaldet på tværs af hver modstand skal du anvende Ohms lovV=Ir.

Disse beregninger giver en klar forståelse af, hvordan spænding er fordelt og strømstrømme i kredsløbet.Denne viden er nødvendig for fejlfinding og optimering af kredsløbsydelse.Ved metodisk analyse af spændingsfald og strømstrøm kan du forbedre den praktiske anvendelse af OHMs lov i mere komplekse seriekredsløbsscenarier, hvilket sikrer præcist og effektiv kredsløbsdesign og vedligeholdelse.
Forenkling af flere modstande til et enkelt ækvivalent
I seriekredsløb er beregning af den samlede modstand ligetil.Det involverer at opsummere modstandene for alle modstande, der er forbundet med ende til ende.Denne teknik forenkler kompleksiteten af elektriske kredsløb, hvilket gør det muligt for dem at blive repræsenteret som en enkelt ækvivalent modstand.Denne forenklede model gør det lettere at analysere og forstå kredsløbets opførsel. Overvej et seriekredsløb med tre modstande: 3 kΩ, 10 kΩ og 5 kΩ.For at finde den samlede modstand tilføjer du blot disse værdier:
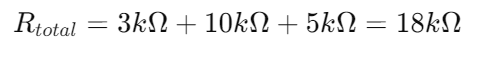
Denne 18 kΩ samlede modstandsmodeller den kombinerede modstand mod den nuværende strøm, der er præsenteret af de tre modstande.
Ækvivalensen af denne opsætning til et kredsløb med en enkelt 18 kΩ modstand forenkler både teoretiske beregninger og praktiske anvendelser.For eksempel, når man designer et kredsløb eller udfører diagnostik, kan ingeniører og teknikere hurtigt estimere spændingsfald, strømstrøm og strømafledning ved hjælp af denne forenklede model.Denne tilgang forbedrer effektiviteten af kredsløbsanalyse og fejlfinding.
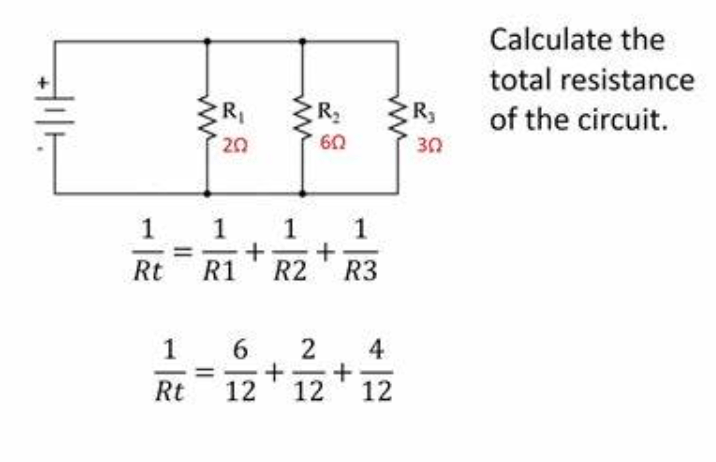
Figur 3: Total modstand i seriekredsløb
At finde ud af total modstand i seriekredsløb
Beregning af den samlede modstand i et seriekredsløb er påkrævet for at forstå kredsløbets samlede elektriske egenskaber, såsom strøm og strømfordeling.I et seriekredsløb tilføjer hver modstand til den samlede modstand, hvilket påvirker, hvor let strømmen kan flyde.Denne ophobning af modstand øger kredsløbets samlede impedans, hvilket reducerer strømmen i henhold til Ohms lov.
For at bestemme den samlede modstand i et seriekredsløb tilføjer du blot modstandsværdierne for alle modstande.For eksempel beregnes den samlede modstand i et kredsløb med modstande til 2 kΩ, 4 kΩ og 6 kΩ som følger:

Denne samlede modstand RTotalpå 12 kΩ fungerer som den enkelte begrænsende faktor for strømmen i hele kredsløbet.
Med den samlede modstandRTotal Kendt kan du beregne den aktuelle, der flyder gennem kredsløbet, når der påføres en bestemt spænding.For eksempel med en 12V strømforsyning, strømmenjeg er:
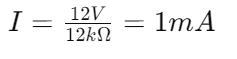
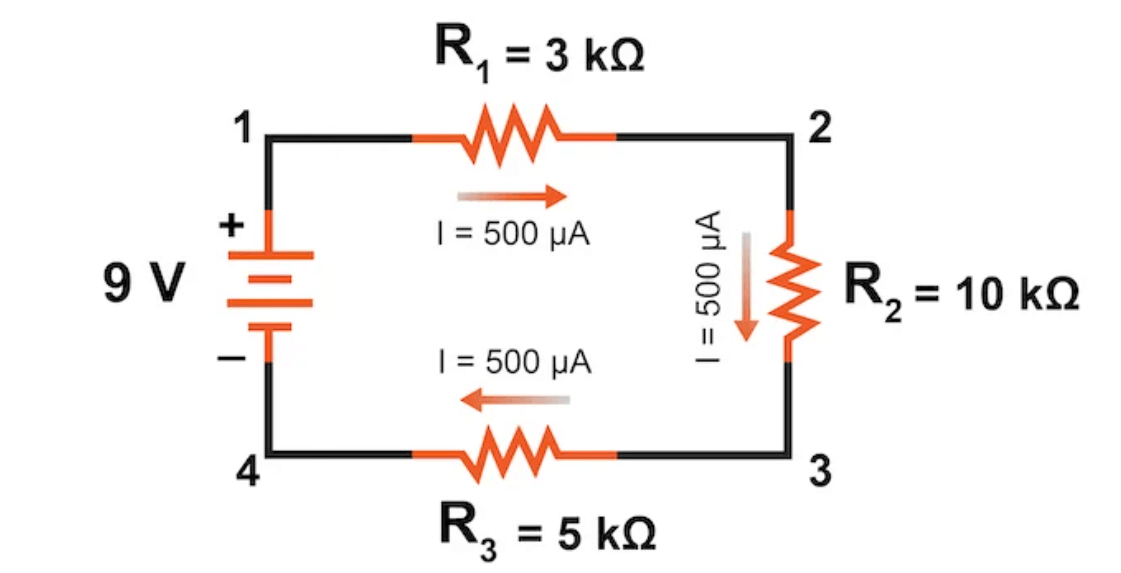
Figur 4: Beregning af kredsløbsstrøm i seriekredsløb
Beregning af kredsløbsstrøm i seriekredsløb
Når du har bestemt den samlede modstand i et seriekredsløb, kan du bruge Ohms lov til at beregne kredsløbets samlede strøm.Denne proces er nøglen til forståelse og styring af kredsløbets ydeevne.Overvej et seriekredsløb med en total modstand på 18 kΩ og en forsyningsspænding på 9V.Brug af Ohms lov, der udtrykkes  , Du kan beregne den aktuelle strømning gennem kredsløbet.I betragtning af disse værdier er beregningen:
, Du kan beregne den aktuelle strømning gennem kredsløbet.I betragtning af disse værdier er beregningen:

Dette resultat, 500 μA, repræsenterer den samlede strøm, der flyder gennem enhver komponent i serien kredsløb.
Det skal opretholdes for at forstå kredsløbets strøm for at vurdere både dens ydeevne og sikkerhed.Dette giver ingeniører og teknikere mulighed for at forudsige dens opførsel under operationelle forhold og designe den for at undgå overbelastning og potentiel fiasko.Præcis strømberegning er primær til fejlfinding, da det hjælper med at identificere problemer som overdreven modstand eller uventede spændingsfald på tværs af komponenter, hvilket indikerer defekte eller nedbrudte dele.Denne analytiske tilgang sikrer kredsløbets effektivitet og pålidelighed.Disse forbedrer også vedligeholdelsesprocedurer med klare målinger for overvågning af kredsløbets sundhed.
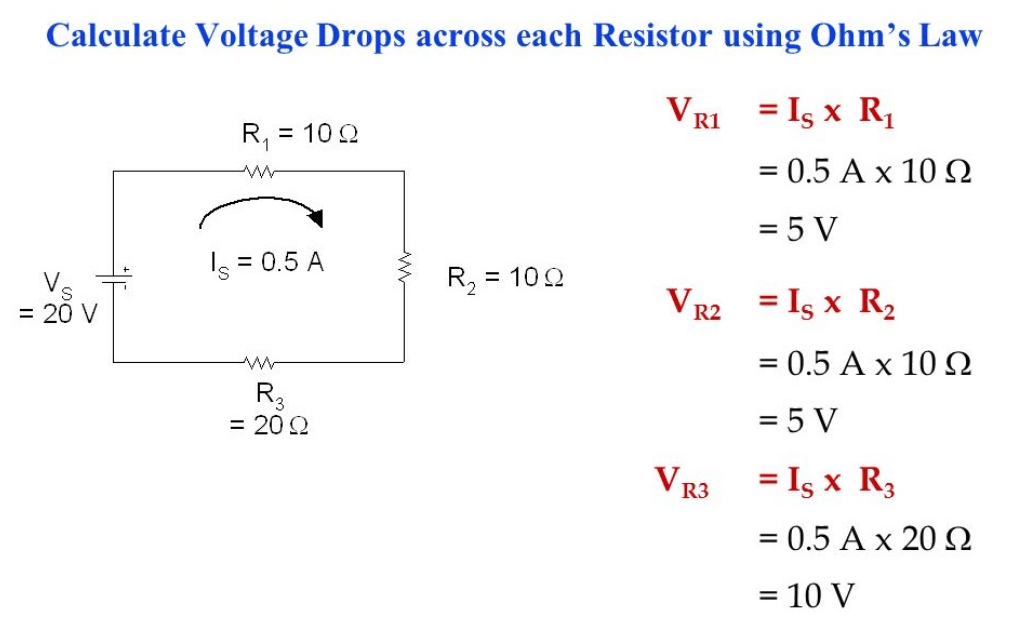
Figur 5: Spændingsfald
Spændingsfaldsanalyse i seriekredsløb
Beregning af spændingsfaldet over hver modstand i et seriekredsløb er ligetil, når du kender den samlede strøm, der strømmer gennem kredsløbet.Spændingsfaldet over enhver modstand er proportional med dens modstand og den samlede strøm efter Ohms lov (V=Ir)
Antag, at den samlede strøm i kredsløbet er 500 μA (0,5 Ma), og modstandene i serie er 3 kΩ, 10 kΩ,

Bekræftelse med Kirchhoffs spændingslovgivning
Summen af disse spændingsdråber er:

Dette matcher den samlede spænding, der leveres af batteriet, hvilket bekræfter Kirchhoffs spændingslov, der siger, at den samlede spænding omkring enhver lukket sløjfe i et kredsløb skal være lig med nul, hvilket tegner sig for spændingsstigninger og dråber.
Seriekredsløbsprincipper
I et seriekredsløb er det ultimative princip, at den samme strøm strømmer gennem hver komponent uden nogen variation.Denne ensartethed er central for at forudsige, hvordan forskellige elementer inden for kredsløbet vil opføre sig under forskellige elektriske belastninger.At vide, at strømmen forbliver konstant, forenkler analysen og design af seriekredsløb.
Et andet hovedkarakteristik ved seriekredsløb er modstandens additive karakter.Den samlede modstand i et seriekredsløb er summen af de individuelle modstande.Denne kumulative modstand påvirker direkte den samlede strømstrøm, som beskrevet af Ohms lov (V=Ir) Jo højere den samlede modstand, jo lavere er strømmen for en given spænding.Denne forbindelse er usikker til at forstå kredsløbets samlede ydelse og effektivitet.
Beregning af spændingsfald
Beregning af spændingsfald over hver komponent er et must.Spændingsfaldet over enhver modstand i et seriekredsløb kan findes ved at multiplicere strømmen med modstandens modstand Summen af disse individuelle spændingsdråber skal svare til den samlede spænding, der leveres af batteriet.Dette bekræfter Kirchhoffs spændingslov, der siger, at summen af alle spændinger omkring enhver lukket sløjfe skal være nul, hvilket sikrer energibesparelse inden for kredsløbet.Det forbedrer deres praktiske anvendelighed i forskellige applikationer, fra enkle elektroniske enheder til komplekse elektriske systemer.
Nøgleprincipper for seriekredsløbsdynamik
Lov om total modstand
Den samlede modstand i et seriekredsløb er summen af alle individuelle modstande langs stien.Denne lov er grundlæggende til beregning af kredsløbets samlede modstand, der direkte påvirker, hvor meget strøm strømmer gennem kredsløbet.For eksempel, hvis et kredsløb inkluderer modstande på 2 kΩ, 3 kΩ og 5 kΩ i serie, den samlede modstand RTotal er:

Denne kumulative modstand er betydelig for at bestemme kredsløbets impedans til den nuværende strøm.
Lov om konstant nuværende
I et seriekredsløb forbliver strømmen konsistent på tværs af hver komponent.Dette betyder, at den samme strøm strømmer gennem enhver modstand, uanset dens modstand.Denne konstance er påkrævet for at sikre, at kredsløbet fungerer forudsigeligt under forskellige belastninger.Det forenkler også analysen og design af seriekredsløb.For eksempel, hvis den samlede strøm, der er beregnet ved hjælp af OHMs lov, er 1 Ma, vil hver komponent i serien opleve denne 1 Ma af strøm.
Lov om spændingsafdeling
Den samlede spænding over kredsløbet er summen af spændingen falder over hver komponent.Dette princip følger Kirchhoffs spændingslov, der hævder, at den samlede sum af spændinger omkring enhver lukket sløjfe i et kredsløb skal være nul.For at sikre korrekt drift og energibesparelse skal du beregne spændingsfaldet over hver modstand ved hjælp af og kontroller, at summen er lig med kildenspænding.
og kontroller, at summen er lig med kildenspænding.
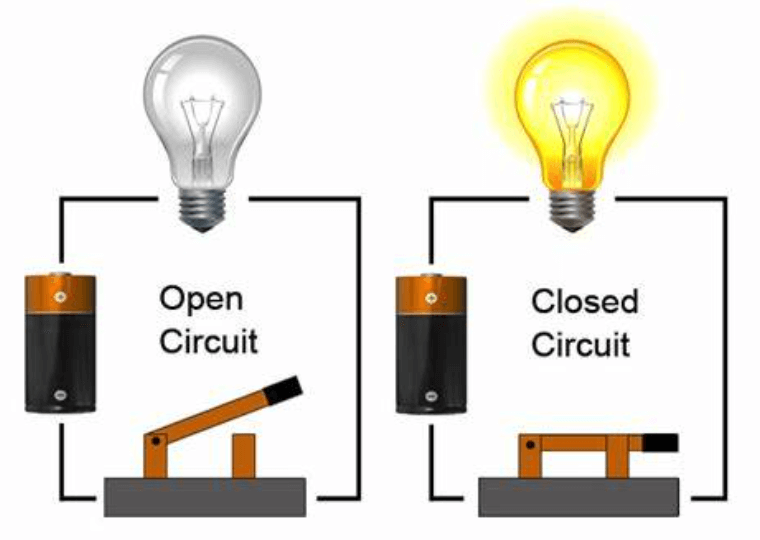
Figur 6: Åben kredsløb
Implikationer af en åben i seriekredsløbskonfigurationer
En åben eller pause, i et seriekredsløb, stopper hele strømmen.Dette forekommer, fordi den kontinuerlige sti, der kræves til elektrisk ladningsstrøm, forstyrres.Når der er en åben, falder strømmen straks til nul, da elektrisk strøm ikke kan krydse huller i kredsløbet.
Når der opstår en åben, er potentialforskellen eller spænding på tværs af pausen lig med den fulde kildespænding.Uden strøm, der flyder gennem modstandene, er der ingen spændingsfald over dem.I stedet vises hele spændingen leveret af kilden over det fri.Lad os sige, at i et kredsløb, der er drevet af et 9V -batteri, ville et åbent resultere i en 9V -måling i pausen.
Denne afbrydelse forhindrer enheden eller belastningen i kredsløbet i at fungere.Det udgør også en risiko for skader på grund af den pludselige eksponering for fuld kildespænding.At forstå virkningerne af et åbent kredsløb er afgørende for fejlfinding og reparation, da det hjælper med at identificere placeringen og arten af kredsløbsfejl hurtigt.
Forståelse af linjedråbe og tab i elektrisk kredsløbsdesign
I kredsløbsdesign, linjedråbe og linjetab har væsentlig indflydelse på ydelsen af elektriske systemer.Disse faktorer hjælper med at sikre kredsløbseffektivitet og pålidelighed, især i langdistance kraftoverførsel eller ved håndtering af følsomt elektronisk udstyr.
Linjedråbe henviser til spændingsreduktionen langs en leder på grund af dens iboende modstand.Flere faktorer bestemmer omfanget af dette spændingsfald:
Dirigentmateriale: Almindeligvis kobber eller aluminium for deres gode ledningsevne og omkostningseffektivitet.
Tværsnitsareal: Et mindre tværsnitsareal resulterer i et højere spændingsfald for den samme strøm.
Længde på lederen: Længere ledere udviser højere spændingsfald.
Linjetab vedrører energi, der er mistet som varme på grund af den ledende vejs modstand.Flere faktorer påvirker dette tab:
Materielle egenskaber og dimensioner: Materialet og størrelsen på lederen påvirker modstand.
Lederens tilstand: Oxidation, fysisk skade eller dårlige forbindelser kan øge modstanden og energitab.
Hvordan minimerer linjespændingsfald og linjetab?
• Valg af passende materialer og størrelser
Vælg ledermaterialer og dimensioner, der minimerer modstand.
• Optimeringslængde på ledende stier
Kortere stier reducerer modstand og tilknyttede tab.
• Opretholdelse af lederintegritet
Sørg for, at forbindelser er sikre, og lederen er i god stand.
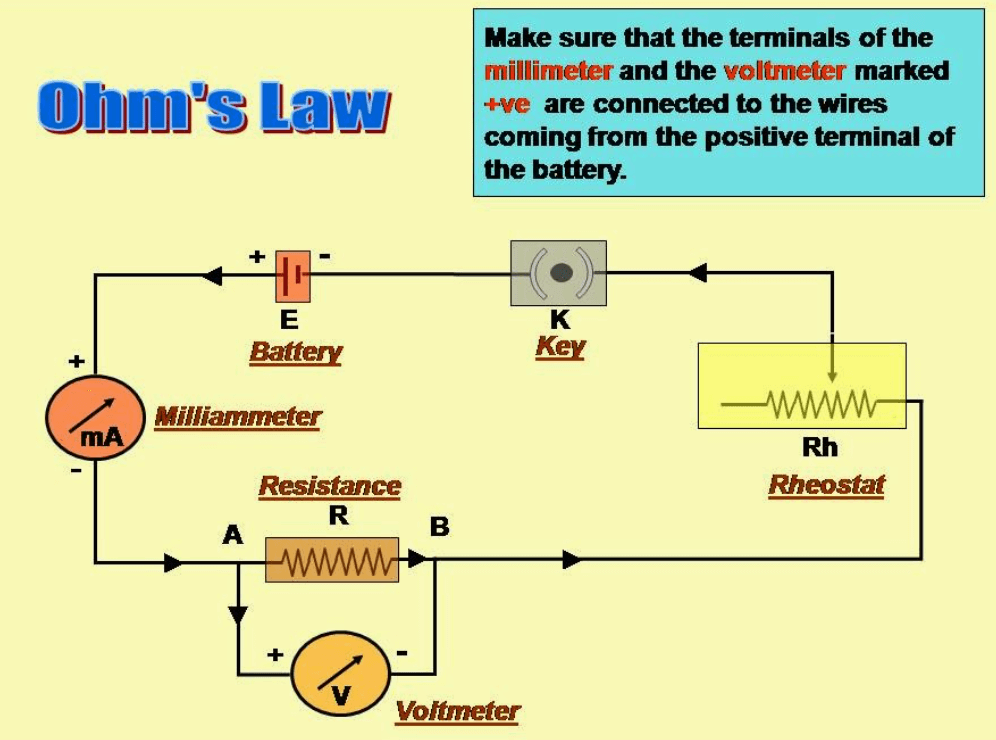
Figur 7: Anvendelse af Ohms lov i kredsløb
Effektiv anvendelse af Ohms lov i kredsløbsanalyse
Ohms lov, givet af (hvor er spænding, er aktuel og er modstand), er nødvendig for at analysere elektriske kredsløb.Korrekt anvendelse er imidlertid afgørende for nøjagtige resultater.Forkert fortolkninger eller forkerte input, især når du blander værdier fra forskellige dele af et kredsløb, kan føre til betydelige fejl.
Spændingen (V), strøm (I) og resistens (R) -værdierne for hver komponent eller segment, der er undersøgt, skal identificeres korrekt for at udføre en nøjagtig kredsløbsanalyse.Dette skyldes, at konfigurationen og egenskaberne ved kredsløbet kan påvirke værdierne for individuelle komponenter og segmenter.Der kræves konsistente målinger;For eksempel, når man måler spændingen over en modstand, skal du sikre dig, at kredsløbet er drevet, og strømmen flyder aktivt gennem denne modstand.Derudover er det nødvendigt med at forstå kontekst og arrangement af komponenter.I seriekredsløb er den samlede modstand summen af individuelle modstande med den samme strøm, der flyder gennem alle komponenter.Omvendt, i parallelle kredsløb, selvom spændingen på tværs af hver gren forbliver konstant, adskiller den totale modstand og den nuværende fordeling sig fra dem i seriekredsløb
Trin for at anvende Ohms lov korrekt
Begynd fejlfinding af et kredsløb ved at identificere dets konfiguration - hvad enten det er serie, parallelt eller en kombination af begge dele.Beregn derefter den samlede modstand ved hjælp af de passende formler til kredsløbstypen.Mål eller bereg derefter spændingen og strømmen, hvilket sikrer, at disse målinger vedrører den samme del af kredsløbet under identiske forhold for at opretholde nøjagtighed.Ved at overholde disse retningslinjer sikrer du nøjagtig kredsløbsanalyse og pålidelige konklusioner om kredsløbets opførsel, ydeevne og sikkerhed.Denne disciplinerede anvendelse af Ohms lov er nyttig til både teoretiske beregninger og praktisk fejlfinding, hvilket gør det nødvendigt for elektriske ingeniører og teknikere.
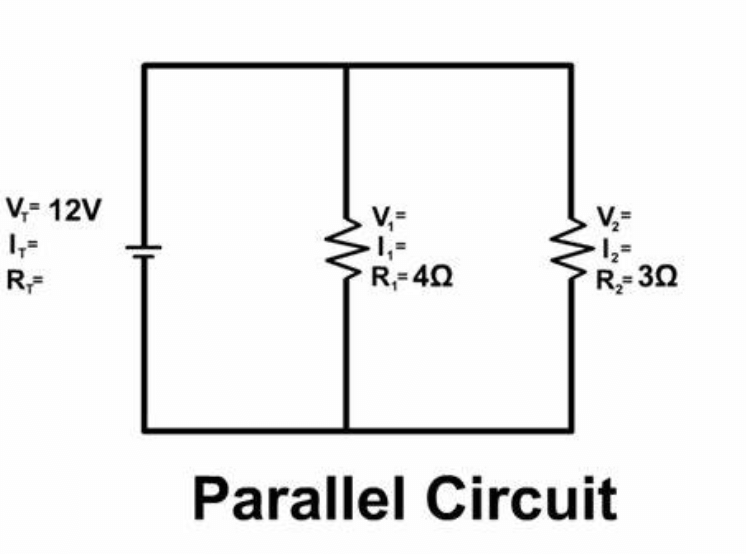
Figur 8: Enkle parallelle kredsløb
Undersøgelse af enkle parallelle kredsløb
Parallelle kredsløb adskiller sig grundlæggende fra seriekredsløb med hensyn til spænding, strøm og modstandsdistribution.
Spændingsuniformitet
I parallelle kredsløb er spændingen over hver komponent eller gren identisk og lig med kildespændingen.Denne ensartethed forenkler spændingsanalyse på tværs af individuelle komponenter, da hver enkelt oplever den fulde spænding af strømforsyningen direkte.
Nuværende distribution
Den samlede strøm, der flyder gennem et parallelt kredsløb, er summen af strømme gennem hver parallel gren.Dette forekommer, fordi kildestrømmen deler sig mellem de flere veje.Brug af Ohms lov , giver dig mulighed for at beregne strømmen i hver gren.Strømmen gennem hver gren afhænger af denne grenes modstand.
, giver dig mulighed for at beregne strømmen i hver gren.Strømmen gennem hver gren afhænger af denne grenes modstand.
Modstandsberegning
Den samlede modstand i et parallelt kredsløb er mindre end modstanden for enhver individuel gren.Dette skyldes, at flere veje giver flere ruter til strømstrøm, hvilket reducerer den samlede modstand mod den nuværende strømning.Den samlede modstand beregnes ved hjælp af formlen:  er modstandene for de enkelte grene.
er modstandene for de enkelte grene.
Konklusion
Udforskningen af seriekredsløb gennem anvendelsen af Ohms lov og andre grundlæggende principper giver dyb indsigt i opførsel af elektriske systemer.Ved at dissekere strømmen af strøm gennem enkelt- og flere modstandsopsætninger får vi en omfattende forståelse af, hvordan spænding, strøm og modstandssamspil for at diktere kredsløbsydelse.Artiklen bekræfter ikke kun konsistensen af aktuelle i seriekredsløb - et afgørende aspekt til at forudsige elektrisk belastningsadfærd - men fremhæver også de praktiske anvendelser ved beregning af total resistens og spændingsdråber, der er nyttige til kredsløbsdesign og fejlfinding.
Udvidelsen af disse principper til parallelle kredsløb og diskussionen på linjetab og spændingsfald i kredsløbsdesign forbedrer vores evne til at optimere, fejlfinde og sikkert opretholde elektriske systemer.Denne grundige analyse sikrer, at både spirende og erfarne ingeniører kan anvende disse koncepter for at forbedre pålideligheden, effektiviteten og sikkerheden af elektriske kredsløb og således imødekomme de hårde krav fra moderne elektroteknik.
Ofte stillede spørgsmål [FAQ]
1. Hvad er anvendelsen af Ohms lov i et seriekredsløb?
Ohms lov er grundlæggende i seriekredsløb for at bestemme strømmen, der flyder gennem kredsløbet, når den samlede modstand og den påførte spænding er kendt.Den siger, at strømmen (i) gennem en leder mellem to punkter er direkte proportional med spændingen (V) på tværs af de to punkter og omvendt proportional med dirigentens modstand (R).I et seriekredsløb, hvor modstande er forbundet med ende til ende, er den samlede modstand summen af de individuelle modstande.Brug af Ohms lov , kan du beregne den enkelt aktuelle værdi, der strømmer gennem hver komponent i serien kredsløb.
, kan du beregne den enkelt aktuelle værdi, der strømmer gennem hver komponent i serien kredsløb.
2. Hvad er anvendelsen af et seriekredsløb?
Serien kredsløb bruges i situationer, hvor driften af en komponent påvirker alle andre, der er forbundet i kredsløbet - tænk af gamle juletrælys, hvor hvis en pære mislykkedes, ville hele strengen gå ud.De er nyttige i applikationer, der kræver spændingsdelere eller aktuelle begrænsende konfigurationer, såsom i grundlæggende elektronisk træning, uddannelsesdemonstrationer og enkle elektroniske projekter.
3. Hvordan fungerer et seriekredsløb?
I et seriekredsløb er alle komponenter forbundet i en lineær sekvens, der danner en enkelt sti for strømmen til at flyde.Den samme strøm strømmer gennem hver komponent, startende fra strømkilden, bevæger sig gennem hver komponent og vender tilbage til strømkilden.Den samlede spænding over kredsløbet er delt mellem komponenterne i henhold til deres modstandsværdier.
4. Hvad er vigtigheden af et seriekredsløb?
Serien kredsløb er nøglen til deres enkelhed og effektivitet i applikationer, hvor ensartet strøm er nødvendig på tværs af flere komponenter.
5. Hvad er de tre regler i et seriekredsløb?
Aktuel regel: Strømmen er den samme gennem alle komponenter i serien.Der er kun en sti for den nuværende strømning, så uanset hvilken strøm kommer ind i en komponent, må også forlade den.
Spændingsregel: Den samlede spænding over seriens kredsløb er summen af spændingerne på tværs af hver komponent.Dette er en konsekvens af bevarelsen af energi.
Modstandsregel: Den samlede modstand for et seriekredsløb er lig med summen af de individuelle modstande for alle komponenter i kredsløbet.Dette påvirker, hvordan den samlede spænding fordeles og størrelsen af strømmen gennem kredsløbet.
Om os
ALLELCO LIMITED
Læs mere
Hurtig forespørgsel
Send en forespørgsel, vi svarer med det samme.

Forståelse af den siliciumstyrede ensretter (SCR)
på 2024-06-07
Schmitt udløser i moderne elektronik: forståelse af deres rolle og evner
på 2024-06-06
Populære indlæg
-
Hvad er GND i kredsløbet?
på 1970-01-01 2946
-

RJ-45 Connector Guide: RJ-45 Stikfarvekoder, ledningsordninger, R-J45-applikationer, RJ-45 datablad
på 1970-01-01 2502
-

Fiberstikstyper: SC vs LC og LC vs MTP
på 1970-01-01 2091
-
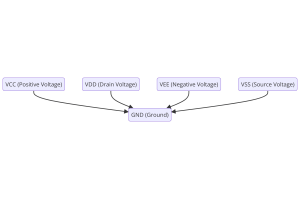
Forståelse af strømforsyningsspændinger i elektronik VCC, VDD, VEE, VSS og GND
på 0400-11-09 1898
-

Sammenligning mellem DB9 og RS232
på 1970-01-01 1765
-

Hvad er et LR44 -batteri?
Elektricitet, den allestedsnærværende kraft, roligt gennemsyrer alle aspekter af vores daglige liv, fra trivielle gadgets til livstruende medicinsk udstyr, det spiller en stille rolle.Imidlertid er det ingen let opgave at gribe ind i denne energi, især hvordan man opbevarer og effektivt udsender den.Det er på denne baggrund, at denne artikel vil fokusere på en type møntcellebatteri, der kan ...på 1970-01-01 1714
-

Forståelse af de grundlæggende elementer: induktansresistens, og kapacitet
I den komplicerede dans inden for elektroteknik tager en trio af grundlæggende elementer centrum: induktans, modstand og kapacitans.Hver bærer unikke træk, der dikterer de dynamiske rytmer af elektroniske kredsløb.Her går vi på en rejse for at dechiffrere kompleksiteten af disse komponenter for at afsløre deres forskellige roller og praktiske anvendelser inden for det store elektriske o...på 1970-01-01 1662
-

CR2430 Batteri Comprehensive Guide: Specifikationer, applikationer og sammenligning med CR2032 -batterier
Hvad er CR2430 -batteri?Fordele ved CR2430 -batterierNormCR2430 Batteri applikationerCR2430 ækvivalentCR2430 vs CR2032Batteri CR2430 størrelseHvad man skal kigge efter, når man køber CR2430 og ækvivalenterDatablad PDFOfte stillede spørgsmål Batterier er hjertet i små elektroniske enheder.Blandt de mange tilgængelige typer spiller møntceller en afgørende rolle, der ofte findes i regnemas...på 1970-01-01 1567
-
Hvad er RF, og hvorfor bruger vi det?
Radiofrekvens (RF) -teknologi er en vigtig del af moderne trådløs kommunikation, der muliggør datatransmission over lange afstande uden fysiske forbindelser.Denne artikel dækker det grundlæggende i RF og forklarer, hvordan elektromagnetisk stråling (EMR) gør RF -kommunikation mulig.Vi vil udforske principperne for EMR, oprettelse og kontrol af RF-signaler og deres omfattende anvendelser.Art...på 1970-01-01 1550
-

CR2450 vs CR2032: Kan batteriet bruges i stedet?
Lithium -manganbatterier har nogle ligheder med andre lithiumbatterier.Høj energitæthed og lang levetid er de egenskaber, de har til fælles.Denne form for batteri har vundet tillid og fordel for mange forbrugere på grund af dens unikke sikkerhed.Dyre tech -gadgets?Små apparater i vores hjem?Se dig omkring, så ser du dem overalt.Blandt disse mange lithium-manganske batterier er CR2450-batteri...på 1970-01-01 1519














































