Hjem Blog~~Detaljeret guide til fuld adder~~

~~på 2024-05-10~~ ~~605~~

Detaljeret guide til fuld adder

På området for digital elektronik og computerteknik repræsenterer tilføjere en af de mest essentielle byggesten, der er vigtige i konstruktionen og funktionaliteten af mere komplicerede aritmetiske kredsløb.Som integrerede komponenter i den aritmetiske logikenhed (ALU) letter tilføjere adskillige computeroperationer, der spænder fra grundlæggende aritmetik til komplekse logiske opgaver, der er nødvendige til systemoperationer.Deres design, der kan variere fra enkle halvtiladrettet til mere komplekse fulde tilføjere, spiller en afgørende rolle i at øge effektiviteten og hastigheden i behandlingen inden for digitale systemer.Denne artikel dykker ned i den detaljerede arkitektur og funktionelle nuancer af forskellige typer tilsættere, der illustrerer deres kritiske rolle i moderne computerteknologi og udforsker deres operationelle logik, kredsløb og applikationer inden for den bredere kontekst af digital logikdesign.

Katalog

1. Hvad er en adder?

2. Halv adder

3. Fuld adder

4. Fuld adder sandhedstabel

5. Egenskaber ligninger af en fuld adder

6. Implementering af et fuldt Adder -kredsløb

7. Fordele og ulemper ved fulde tilføjere

8. Anvendelser af fulde tilføjere i digital logik

9. Eksempler på fuld adder -implementering

10. Konklusion

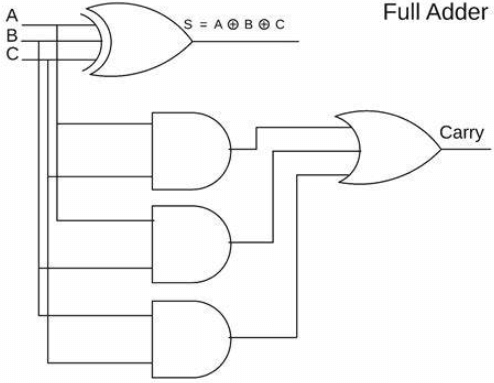
Figur 1: Fuld adder

Hvad er en adder?

En adder er en grundlæggende komponent inden for elektronisk teknik og digital logisk design og spiller en central rolle i mere komplekse computersystemer.Som en del af den aritmetiske logikenhed (ALU) håndterer Adder en række vigtige computeropgaver.Effektiviteten og ydeevnen for hele processoren påvirkes direkte af design og funktionalitet af adder.

I processoren bruges adder ikke kun til grundlæggende aritmetiske operationer som tilføjelse og subtraktion, men den engagerer sig også i en bredere række logiske operationer.For eksempel, når man kører programmer, skal processoren ofte beregne nye hukommelsesadresser.Dette gøres typisk ved at tilføje eller trække fra den aktuelle adresse - en opgave, der udføres af Adder.De kontrollerer antallet af loop -iterationer og den samlede strøm ved at øge og dekrementerende tællere.I mere komplekse applikationer, såsom tabelindeksering, lokaliserer tilføjere hurtigt data ved at beregne forskydninger.Dette er vigtigt for databasestyringssystemer, kompileringskonstruktion og storskala databehandling.Tilsættere er også nøglen til implementering af visse kortlægningsteknikker i cache-systemer på flere niveauer ved hjælp af aritmetiske operationer til at bestemme placeringen af data i cachen og dermed optimere adgangseffektiviteten.

Teknologisk implementeres tilføjere gennem forskellige kredsløbsdesign, herunder parallelle, serielle og rørledningstilsættere.Parallelle tilføjere foretrækkes for deres evne til at håndtere flere cifre samtidigt, hvilket gør dem velegnede til scenarier, der kræver hurtig beregning.Serielle tilføjere behandler på den anden side en bit pr. Urcyklus og er ideelle til ressourcebegrænsede miljøer med lav effekt.Pipeline -tilføjere deler tilføjelsesprocessen i flere faser, der hver håndterer en del af tilføjelsesoperationen.Dette design øger beregningshastigheden markant, især i høje præstationsberegningsmiljøer.

Halv adder

Et halvt adder kredsløb er en grundlæggende byggesten i digital elektronik, specielt designet til at tilføje to enkelt binære cifre.Dette kredsløb danner grundlaget for en fuld adder og er nøglen til at forstå mere komplekse logiske kredsløbsdesign.I en halv adder er der to primære input, mærket A og B, der repræsenterer henholdsvis Augend og tillæg.Denne opsætning gør det muligt for den at beregne summen og bære output uden behov for en bæringsindgang fra tidligere beregninger.

Kernen i et halvt vagt består af to logiske porte: en Xor-port og en og gate.XOR -porten er ansvarlig for at generere SUM -output.Det fungerer under en simpel regel, hvor den udsender en 1, hvis kun en af dens input er 1;Ellers udsender den en 0. og porten på den anden side håndterer bæreproduktionen.Det producerer kun 1 1, når begge dens input er 1, der tilpasser sig perfekt med de grundlæggende krav til binær tilføjelse.

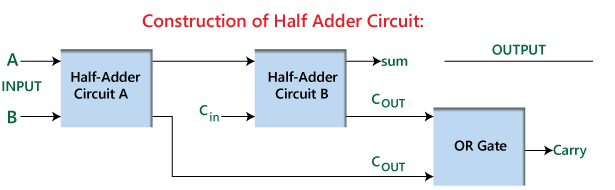
Figur 2: Konstruktion af halv adder

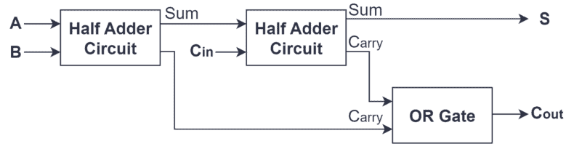
Dette effektive og ligetil design giver den halve adder ikke kun mulighed for at udføre grundlæggende binær tilføjelse uafhængigt, men også at fungere som en byggesten til at skabe en fuld adder.En fuld adder er konstrueret ved at kombinere to halvt tilføjere med en ekstra eller port.I denne opsætning påtager den første halvdel Adder den indledende tilføjelsesopgave og genererer en foreløbig sum og bære.Den anden halvdel Adder behandler derefter bæren fra den første sammen med en ekstra bæreindgang.Endelig fusionerer OR -porten, at de to bærer output for at producere den endelige bærende output.Dette arrangement forbedrer adderens funktionalitet, hvilket gør det muligt for den at håndtere mere komplekse multi-bit-tilføjelseopgaver, der viser den udbredte anvendelse og betydning af halvtilsættere i digitalt kredsløbsdesign.

Fuld adder

En fuld adder er en avanceret komponent i digital logikdesign, udstyret til at håndtere tilføjelsen af tre enkeltbitiske binære input, der ofte er mærket som A, B og overførsels (CIN).Dette design giver den fulde adder mulighed for effektivt at behandle komplekse binære tilføjelser ved at inkorporere bæren fra tidligere lavere ordens beregninger i en enkelt operation.

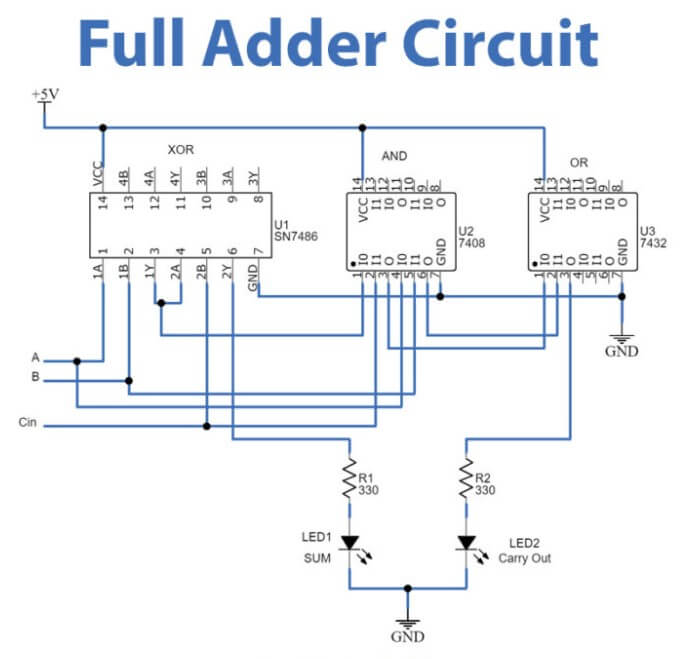
Figur 3: Fuld adder -kredsløb

Funktionelt kan en fuld adder udsende en tocifret sum, hvilket betyder, at dens output kan variere fra 0 til 3, og den kan også producere en gennemførelse (cout).Dette sker, fordi når alle inputbits er indstillet til 1 (a = 1, b = 1, cin = 1), vil summene output være 1 (der repræsenterer binær 01), og en gennemførelse af 1 genereres, hvilket indikerer detEn ekstra bære skal overføres til den næste højere bit.

Strukturelt består den fulde adder generelt af to halvt tilføjere og en eller port.Den første halvdel-adder tager input A og B og genererer en indledende sum og et bæresignal.Denne indledende sum fodres derefter sammen med indførelsen (CIN) ind i anden halvdel.Den anden halvdel Adder's rolle er at tilføje dette beløb fra første halvdel Adder til CIN, der producerer en anden sum og en ny bæreproduktion.Samtidig fusionerer bærens output fra den første halvdel-adder og bæreproduktionen fra anden halvdel-adder gennem en OR-eller-gate, der kulminerer med den endelige gennemførelse (cout) af den fulde adder.Designet af denne struktur sikrer, at den fulde adder effektivt håndterer forplantningen af luftfartsselskaber derudover operationer, hvilket gør den ideel til udførelse af binære tilføjelser med flere bitiske tilføjelser.Således fremskynder designet af den fulde adder ikke kun databehandling og forbedrer effektiviteten, men forenkler også kompleksiteten af hardwareimplementering gennem en ligetil kombination af logiske porte, hvilket gør det til en uundværlig komponent i multi-cifret tilføjelse og den aritmetiske logiske enhed (ALU).

Parametre	Halv adder	Fuld adder
Beskrivelse	Halv adder er en kombinationslogik kredsløb, der tilføjer to 1-bit cifre.Halv-vejen producerer en sum af de to input.	En fuld adder er en kombinationslogik Circuit, der udfører en tilføjelse af tre binære numre med en binær. Den fulde adder producerer en sum af de tre input og bæreværdi.
Tidligere bære	Den forrige bære bruges ikke.	Den forrige bære bruges.
Input	I en halv adder er der to inputbits (a, B).	I fuld adder er der tre inputbits (A, b, c_i).
Output	Den genererede output er af to bit-sum og bære fra input af 2 bit.	Den genererede output er af to bit-sum og bære fra input af 3 bit.
Brugt som	Et halvt kredsløb kan ikke bruges i på samme måde som et fuld-adder kredsløb.	Et fuldt adder -kredsløb kan bruges på plads af et halvt adder -kredsløb.
Funktion	Det er enkelt og let at implementere	Designet af en fuld adder er ikke som Enkel som en halv adder.
Logisk udtryk	Logisk udtryk for halv adder er: S = a⊕b;C = a*b.	Logisk udtryk for fuld adder er: S = a⊕b⊕cin;C_ud= (ab)+(c_i(a⊕b)).
Logikporte	Det består af en ex-eller-port og en og Port.	Det består af to ex-eller, to og porte, og en eller port.
Applikationer	Det bruges i regnemaskiner, computere, digitale måleenheder osv.	Det bruges i flere bittilsætninger, digitale processorer osv.
Alternativ navn	Der er ikke noget alternativt navn på halvdelen adder.	En fuld adder er også kendt som en krusning-bære adder.

Diagram 1: Forskel mellem den halve adder og fuld adder

Fuld adder sandhedstabel

Sandhedstabellen for en fuld adder er nøglen til at forstå dens operationelle logik, der beskriver det nøjagtige forhold mellem binære inputkombinationer og deres tilsvarende output.Denne tabel demonstrerer alle potentielle input -scenarier og deres resultater, hvilket gør det til et vigtigt værktøj i design og verifikation af digitale logiske kredsløb.Den fulde adder behandler tre input: A, B og en indførsler (CIN), som hver kan være enten 0 eller 1. Dette resulterer i otte mulige kombinationer af input.

For hver af disse kombinationer inkluderer output fra den fulde adder en sum (sum) og en udarbejdelsen (cout).Summen er Modulo-2-tilføjelsen (XOR-drift) af de tre input-A, B og CIN.Udførelsen opstår, når mindst to af inputbitene er 1. Dette afspejler den fulde Adders evne til at håndtere overførslen i sekventielle tilføjelsesoperationer, hvilket sikrer nøjagtighed i beregninger med højere bit.

For at illustrere skal du overveje input-scenariet, hvor alle input er 0 (a = 0, b = 0, c-in = 0).Outputsummen vil være 0, og bæren vil også være 0, hvilket indikerer, at der ikke er nogen yderligere sum eller bære at administrere.Hvis kun en inputbit er 1, såsom a = 1, b = 0, c-in = 0, vil outputsummen være 1 uden bærer, hvilket viser, at der ikke er behov for at overføre en bær til en højere bit.Når to inputbits er 1, som a = 1, b = 1, c-in = 0, er outputsummen 0 (siden 1+1 er lig med 2 i binær, og modulo-2 resulterer i 0), men transportenUd er 1, der angiver en bære, der skal overføres til den næste højere bit.Det mest komplekse scenarie opstår, når alle tre inputbits er 1 (a = 1, b = 1, c-in = 1);Outputsummen er 1, og der er en gennemførelse af 1, hvilket antyder, at bærestyring også kan være påkrævet på endnu højere bits.

EN	B	C_i	S	C_ud
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Diagram 2: Fuld Adder Truth Table

Karakteristika -ligninger for en fuld adder

At forstå den fulde adder involverer at dissekere dens funktionalitet ved hjælp af sandhedstabellen, hvor forskellige kombinationer af inputværdier A, B og C-in fører til output sum og cout.For at forstå operationen forenkler vi de logiske ligninger trin for trin.

Logisk udtryk for sum

Ligningen starter med de forskellige tilfælde, hvor summen er lig med 1:

• a 'b' cin + a 'b cin' + a b 'cin' + ab cin

Denne ligning kan kondenseres ved at gruppere termer med og uden CIN:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

Denne forenkling fører til en lettere at implementere form:

• CIN XOR (A XOR B)

Denne repræsentation viser, at sumproduktionen i det væsentlige er XOR -operationen blandt A, B og CIN, der fanger kerneadfærd for binær tilføjelse, hvor summen skifter baseret på et ulige antal dem.

Logik til cout

Start med forhold, hvor bæren genereres:

• a 'b cin + a b' cin + ab c-in ' + ab cin

Forenkling af ligningen identificerer vi udtryk, der ofte involverer at generere en bære:

• AB + B CIN + A CIN

På udkig efter en anden metode til implementering af cout, kan ligningen omorganiseres:

• AB + A CIN + B C-IN (A + A ')

Dette udvides og rekombiner til at fange alle scenarier, hvor mindst to input er 1:

• ab cin + ab + a c-in + a 'b cin

• AB (1 + CIN) + A C-in + A 'B CIN

• AB + A C-in (B + B ') + A' B CIN

• ab + a b 'cin + a' b cin

• AB + CIN (A 'B + A B')

Den endelige kompakte form for cout:

• AB + CIN (A XOR B)

Denne version af gennemførelsesligningen viser, hvordan cout produceres enten når både A og B er 1, eller når en af A eller B er 1 sammen med en indførelse, og dermed indkapsler den logik, der er nødvendig for at styre bærepropagation i multi-Bit binær tilføjelse.Denne strømlinede logik er især nyttig til implementering af effektive digitale kredsløb.

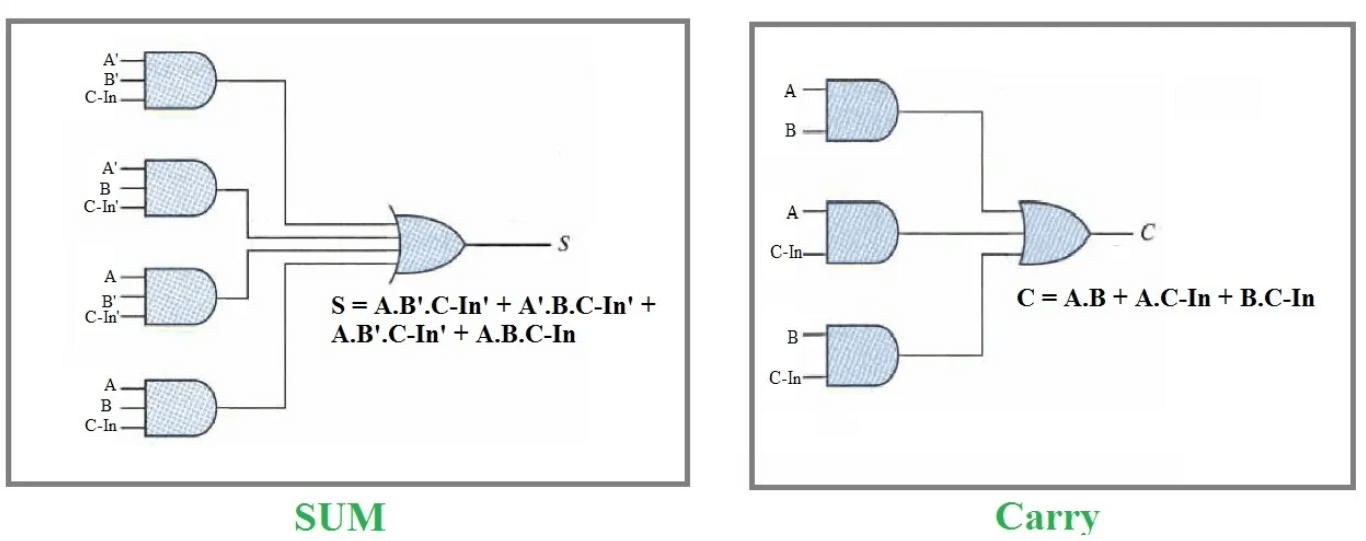
Figur 4: Ligninger af en fuld adder

Implementering af et fuldt Adder -kredsløb

Implementering af et fuldt Adder-kredsløb involverer omhyggeligt at samle to halvt tilføjere og en eller gate for at skabe en enhed, der er i stand til effektivt at håndtere tilføjelsen af tre enkeltbit binære input.Denne ordning optimerer kredsløbets kompleksitet og sikrer både effektive og nøjagtige beregninger.

For at starte med tager den første halvdel Adder to primære binære input, A og B, som er de vigtigste cifre, der skal tilføjes.Dens vigtigste opgave er at beregne summen og den oprindelige bære af disse to numre.Her leverer den første halvdel Adder to resultater: en indledende sum (sum1) og en indledende bære (bær1).Sum1 er afledt af XOR -betjeningen af A og B, hvilket indikerer, om det samlede beløb har et ulige antal 1'er.Bær1, resultatet af og operationen mellem A og B, angiver, om begge cifre er 1, hvilket kræver en bære til den næste højere bit.

Dernæst slutter den anden halvdel Adder sig til processen.Den bruger SUM OUTPUT SUM1 og den tredje input CIN (indførelse fra en tidligere beregning) som dens input.Den anden halvdel Adder producerer to output: det endelige sumresultat (SUM2) og den sekundære bær (bær2).Sum2, som er XOR -resultatet af sum1 og CIN, repræsenterer den endelige sum af de tre input, der viser den aggregerede binære tilføjelse.Carry2, der opstår fra og -operationen mellem sum1 og CIN, indikerer en bærer genereret af disse komponenter.

Full Adder Circuit with Using Two Half Adder

Figur 5: Fuld adder -kredsløb med brug af to halve adder

Endelig, for at afslutte det fulde Adder's design, kræves en OR -gate for at håndtere transportpunkterne bær1 og bære2 fra begge halvt tilføjere.Denne eller gate sikrer, at enhver bær, der genereres under beregningerne, videresendes korrekt til den endelige output.Derfor er den fulde Adders endelige bæreproduktion (cout) OR -resultatet af Carry1 og Carry2.Inkluderingen af denne eller gate garanterer, at alle potentielle bærer beregnes nøjagtigt og formidles til det næste niveau i multi-bit tilføjelsesoperationer, hvilket sikrer integriteten af den aritmetiske operation på tværs af flere bits.

Fordele og udfordringer ved fulde tilføjere i digital logik

Fuldt tilføjere spiller en uundværlig rolle i digital logikdesign og giver adskillige fordele, der gør dem vigtige i forskellige computing- og databehandlingsscenarier.Deres primære fordele inkluderer bemærkelsesværdig fleksibilitet, hurtige behandlingshastigheder og effektiv bærestyring.Disse træk gør fulde tilføjere ideelle til at udføre komplekse aritmetiske operationer og logiske funktioner, især til applikationer, der kræver sekventiel multi-bit tilføjelse.

Fordele

Fleksibilitet: Fuldt tilføjere udmærker sig i deres evne til at behandle flere binære input (A, B og CIN) samtidig.De kan også udvides til større adder -arrays for at håndtere længere binære tal.Denne skalerbarhed er vigtig for at opbygge aritmetiske logiske enheder med høj ydeevne (ALUS), som skal udføre komplicerede multi-bit aritmetiske og logiske operationer.

Hastighed: Takket være deres interne parallelle behandlingsarkitektur kan fulde tilføjere fuldføre tilføjelsen af alle input i en enkelt urcyklus, mens de også bestemmer at udføre output.Denne kapacitet understøtter kontinuerlige tilføjelsesoperationer og er uundværlige til realtid databehandling i moderne mikroprocessorer og højhastigheds computing-enheder.

Ulemper

Imidlertid præsenterer fulde tilføjere også bemærkelsesværdige ulemper:

Kompleksitet i design og implementering: Fuldt tilføjere involverer flere logiske porte og multi-niveau bæreformering, hvilket gør deres designkompleks.Denne kompleksitet øger ikke kun produktionsomkostningerne, men kan også påvirke kredsløbets pålidelighed.

Problemer med udbredelsesforsinkelse: Bær forplantning kan passere gennem flere logiske porte, der hver tilføjer dens forsinkelse.Dette kan begrænse den samlede beregningshastighed under store operationer, især i omfattende computersystemer og i designet af meget stor integration (VLSI) og højhastighedsprocessorer.Forsinkelsen kan blive en betydelig flaskehals i ydelsen.

For at afbøde disse problemer udforsker ingeniører kontinuerligt mere effektive kredsløbsdesign.Strategier inkluderer anvendelse af hurtigere logiske gate-teknologier, optimering af kredsløbslayouts til at forkorte sti-længder og udvikle avancerede teknologier som bærebesparede tilføjere for at minimere forsinkelser i bærepropagation.

Anvendelser af fulde tilføjere i digital logik

Fuldt tilføjere bruges i vid udstrækning i digital logik, værdsat for deres fleksibilitet og effektivitet, hvilket gør dem centrale for et væld af computer- og databehandlingsopgaver.Deres anvendelse spænder fra grundlæggende aritmetiske operationer til kompleks signalbehandling og systemstyring.Her er et detaljeret kig på nogle nøgleområder, hvor fulde tilføjere er integrerede.

Aritmetiske kredsløb

En af de mest ligefremme anvendelser af fulde tilføjere er i aritmetiske kredsløb, hvor de udfører binær tilføjelse.Specielt afgørende i tilføjelse af flere bitnummer, fuldt tilføjere administrerer længere binære sekvenser gennem cascading.I dette arrangement håndterer hver fuld adder tilføjelsen til sin bitposition og bæren fra den nedre bit, og overfører derefter den nye bære til den næste højere bits fulde adder.Denne kaskade muliggør omfattende multi-bit-tilføjelse på tværs af hele cifrene.

Databehandling

Fuldt tilføjere spiller også en central rolle i avancerede databehandlingsopgaver såsom digital signalbehandling (DSP) til filtrering og Fourier -transformationer, hvor der er behov for præcise og hurtige aritmetiske operationer.Derudover inden for informationssikkerhed, herunder datakryptering og fejldetektion og korrektionsalgoritmer som paritetskontrol og Cyclic Redundancy Check (CRC) kodegenerering, er fulde tilføjere afgørende for at udføre vigtige bit -operationer.

Tællere

I digitale tællere er fulde tilføjere uundværlige til implementering af både forøgelse og reduktionsfunktioner, især i modulære og synkrone tællere.De administrerer nøjagtigt bærer og låner for at sikre præcis tælling.

Multiplexers (MUX) og Demultiplexers (Demux)

I multiplexere og demultiplexere spiller fulde tilføjere en kritisk rolle i kanaludvælgelse og datafordeling.De deltager i den logik, der bestemmer, hvilke kanaler der bruges til dataindgang og output, hvilket træffer beslutninger baseret på logiske kontrolsignaler.

Hukommelsesteknologi

Til hukommelsesadresse hjælper fulde tilføjere med at generere adressesignaler til dynamisk adgang til hukommelsessteder.Dette er især vigtigt i Dynamic Random-Access Memory (DRAM) og andre lagringssystemer, hvor fulde tilføjere understøtter komplekse adresserberegninger for at forbedre effektiviteten af hukommelsesadgang.

Aritmetiske logiske enheder (ALU)

Endelig, som grundlæggende komponenter af aritmetiske logiske enheder i mikroprocessorer og digitale signalprocessorer, er fulde tilføjere afgørende.ALU håndterer alle aritmetiske og logiske operationer, med fulde tilføjere, der sikrer, at data behandles både hurtigt og nøjagtigt.

Eksempler på fulde adder -implementeringer

Fuldt tilføjere kan konstrueres ved hjælp af forskellige logiske porte og konfigurationer.Her udforsker vi fire forskellige implementeringer og fremhæver deres opsætning og operationelle nuancer.

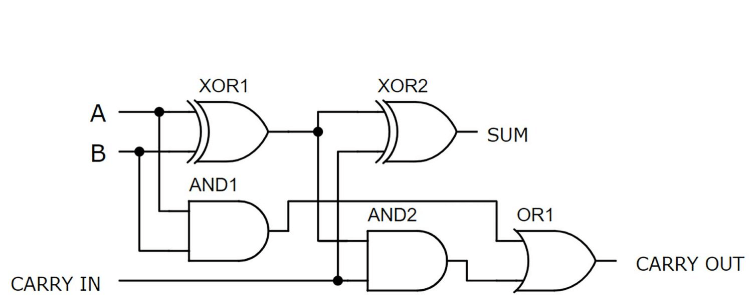
Fuld adder bygget med Xor og, og eller porte

Full Adder Built with XOR, AND, and OR Logic Gates

Figur 6: Fuld adder bygget med XOR, og og eller logiske porte

Dette eksempel viser en fuld adder bygget på et brødbræt ved hjælp af diskrete transistorer.Konfigurationen omfatter fem logiske porte: to Xor -porte, to og porte og en eller gate, der kræver i alt 21 transistorer.Input A og B er tilsluttet til brødbrættets øverste venstre og modtager en +5V -forsyning.Disse input styres ved hjælp af to skiftafbrydere.To lysdioder øverst til venstre angiver tilstandene af input A og B, mens to LED'er på højre side viser output.Modstandene, der bruges i kredsløbet, er alle 2,2 000 ohm.Når input A og B er tændt, og indførelsen er slukket, viser output en binær værdi på 10, der repræsenterer summen 2 (1 + 1 + 0 = 10).XOR-porte, bygget med de første 12 transistorer, håndterer den primære summering, mens den nedre halvdel af brødbrættet indeholder og og eller porte til bærebetjening, farvekodede ledninger forbedrer klarhed og fejlfinding.

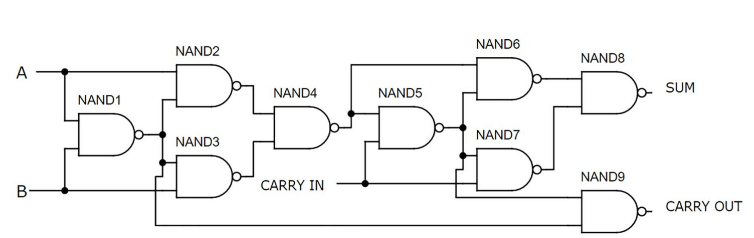
Fuld adder ved hjælp af Nand Gates

Figur 7: Fuld adder ved hjælp af Nand Gates

Denne fulde adder bruger ni NAND -porte, med hver port lavet af to transistorer, i alt 18 transistorer.Denne metode er blandt de enkleste og mest effektive måder at konstruere en fuld adder ved hjælp af diskrete komponenter.Alle porte er samlet på den øverste halvdel af brødbrættet, mens switches optager den nedre halvdel.Kredsløbets funktionalitet demonstreres med input A og B ON og indførelsen af, hvilket resulterer i en output-binær værdi på 10, svarende til decimal 2.

Fuld adder med eller porte

Figur 8: Fuld adder med eller porte

Konstrueret med ni eller porte, der hver kræver to transistorer, bruger denne opsætning også 18 transistorer i alt.At opbygge en fuld adder med Nor Gates tilbyder et godt alternativ, men involverer mere komplekse ledninger sammenlignet med Nand Gates.Hver transistor i Nor -porte er jordet med de samler, der er forbundet med orange jumper -ledninger for at sikre pæne og organiserede ledninger.Denne konfiguration vises med input A og B aktiveret, og indførsler deaktiveres, hvilket fører til output, hvor bæren er aktiv og summen er slukket.

Konklusion

Gennem denne udforskning af AdDer -teknologi, fra basale halvtilsættere til sofistikerede fulde Adder -design, er det tydeligt, at disse komponenter er grundlæggende for fremme af digital elektronik.De operationelle egenskaber og implementeringseksempler gav understreget alsidigheden og effektiviteten af tilføjere i forskellige beregningsmæssige indstillinger.Ved at undersøge strukturen og funktionen af tilføjere, især gennem deres sandhedstabeller og karakteristiske ligninger, får vi værdifuld indsigt i deres evner og begrænsninger.Denne viden er medvirkende til at fremme designet af mere effektive og hurtigere computersystemer.I sidste ende forenkler tilføjere ikke kun komplekse binære beregninger, men muliggør også spredning af teknologi inden for områder så forskellige som databehandling, hukommelsesallokering og digital signalbehandling.Efterhånden som digital teknologi udvikler sig, vil den igangværende forfining og innovation inden for Adder Design fortsat være en hjørnesten i udviklingen af mere avancerede beregningsmæssige arkitekturer, hvilket sikrer, at disse grundlæggende komponenter forbliver i hjertet af digital systemdesign og implementering.

Ofte stillede spørgsmål [FAQ]

1. Hvad er et fuldt Adder -kredsløb?

En fuld adder er et digitalt kredsløb, der tilføjer tre binære bits til at producere en sum og en bærende output.Det er designet til at håndtere tilføjelsen af tre input: to betydelige bits og en indførselsbit fra en tidligere tilføjelse.Dette gør det muligt at bruge det i successive faser til at tilføje binære numre med flere bit.

2. Hvor mange og, eller, xor i fuld adder?

En typisk fuld adder indeholder:

To Xor -porte til generering af summen.

To og porte til at bidrage til udførelsesberegningen.

En eller port til at afslutte udførelsesudgangen.

3. Hvad er bæreindgang i fuld adder?

Bærindgangen (CIN) i en fuld adder er bærebiten fra tilføjelsen af de tidligere lavere betydningsfulde bits i multi-bit binær tilføjelse.Det giver den fulde adder mulighed for at overveje denne tidligere bære, når man beregner den aktuelle sum og den nye gennemførelse.

4. Hvorfor bruge en fuld adder i stedet for en halv adder?

En fuld adder bruges i stedet for en halv adder, fordi den kan tilføje tre bits (inklusive bæren fra tidligere tilføjelser), hvilket gør det velegnet til at kæde sammen for at tilføje multi-bit-numre.En halv adder kan kun tilføje to bits og har ikke en bestemmelse om en indførelse, hvilket begrænser brugen til de enkleste former for binær tilføjelse uden sekventiel bærepropagation.

Om os

ALLELCO LIMITED

Allelco er en internationalt berømt one-stop Indkøbstjeneste Distributør af hybrid elektroniske komponenter, der er forpligtet til at levere omfattende komponent indkøb og forsyningskædeservices til de globale elektroniske fremstillings- og distributionsindustrier, herunder globale top 500 OEM -fabrikker og uafhængige mæglere.
Læs mere