Lavpas filtre afsløret: En omfattende guide til deres funktion og påvirkning
Fremskridt med lavpasfiltre repræsenterer et betydeligt skridt inden for elektronik og lydteknik, hvilket muliggør præcis manipulation og forbedring af frekvensresponser på tværs af et utal af applikationer.Disse filtre, hvad enten det er induktive, kapacitive eller en sofistikeret sammensmeltning af komponenter, tjener som seriøse værktøjer til at afbøde uønsket højfrekvente støj, mens de bevarede de krævede lavere frekvenser.Essensen af lavpas filterteknologi ligger i dens evne til at diskriminere frekvenser, en funktion, der er eventuel i forskellige sektorer, der spænder fra sofistikerede elektroniske kredsløb til nuancerede lydproduktionsmiljøer.Ved at udforske den tekniske mekanik i forskellige lavpasfiltre, herunder deres konstruktion, operationelle principper og de matematiske underbygninger gennem overførselsfunktioner, udforsker denne artikel det brede spektrum af lavpasfilterapplikationer og deres dybe indflydelse på forbedring af systemets ydeevne, signalintegritetog auditiv æstetik.
Katalog
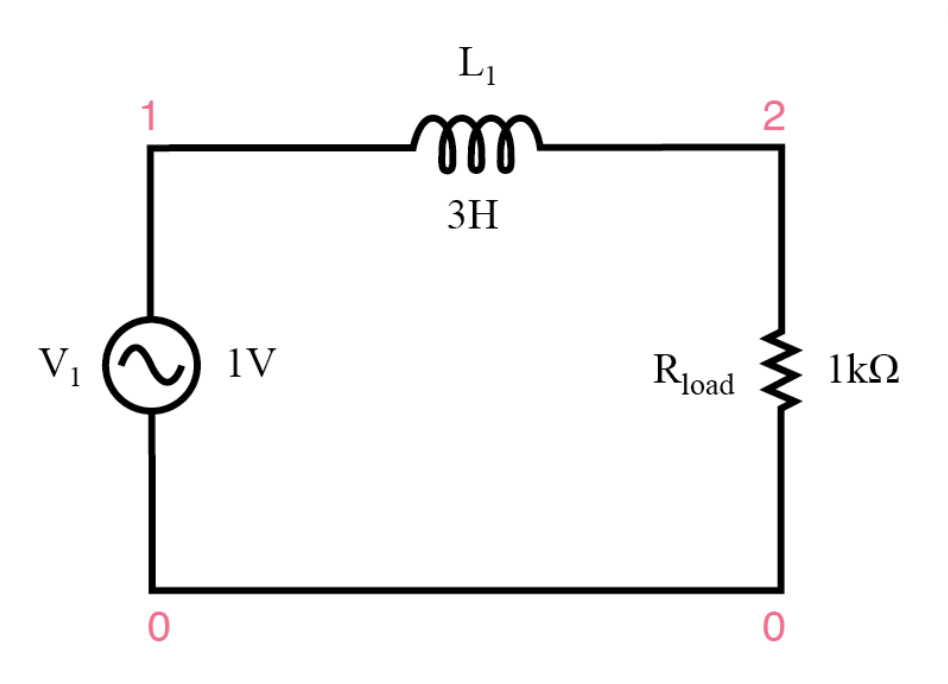
Figur 1: Induktive lavpasfiltre
Mekanikken i induktive lavpasfiltre
Induktive lavpasfiltre er påkrævet til styring af frekvensfordeling inden for kredsløb.De er yderst effektive til at reducere højfrekvente signaler, mens de tillader lavere frekvenser at passere.Kernekomponenten i disse filtre er en induktor, der øger dens impedans, når signalfrekvensen stiger.Denne egenskab gør det muligt for induktoren at virke som en frekvensafhængig modstand, hvilket øger resistensen ved højere frekvenser.
En induktors impedans kan udtrykkes som 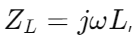 , hvor er vinkelfrekvensen og
, hvor er vinkelfrekvensen og er induktansen.Som vinkelfrekvens
er induktansen.Som vinkelfrekvens  Stiger, det gør impedansen, hvilket gør det bedre til at blokere høje frekvenser.Omvendt forbliver impedansen ved lavere frekvenser lav, hvilket gør det muligt for disse signaler let at passere gennem.
Stiger, det gør impedansen, hvilket gør det bedre til at blokere høje frekvenser.Omvendt forbliver impedansen ved lavere frekvenser lav, hvilket gør det muligt for disse signaler let at passere gennem.
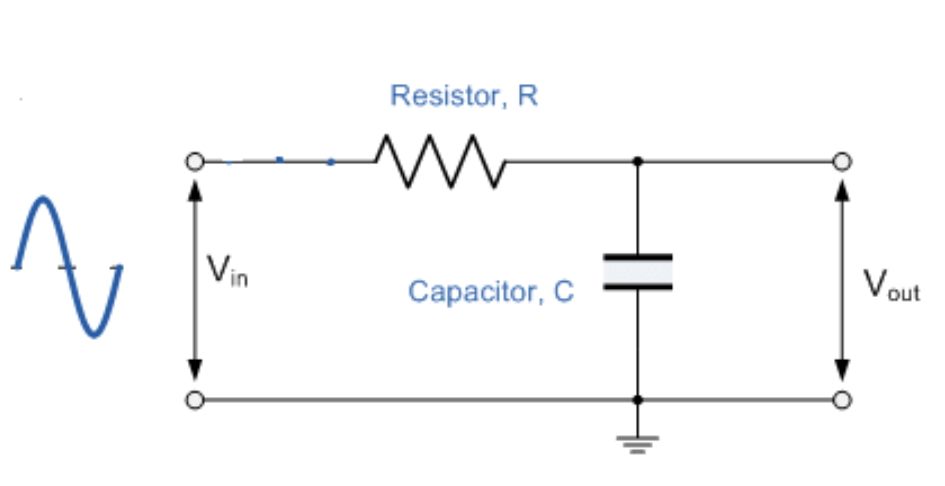
Figur 2: Kapacitive lavpasfiltre
Karakteristika for kapacitive lavpasfiltre
Kapacitive lavpasfiltre bruger de unikke egenskaber hos kondensatorer, der viser faldende impedans, når signalfrekvensen øges.Ved at placere kondensatoren parallelt med belastningen skaber disse filtre en sti, der dirigerer højfrekvente signaler væk fra output.Høje frekvenser absorberes derefter af en formidlingsmodstand, kendt som R1, som adskiller dem fra induktive lavpasfiltre.
Dette filter består typisk af kun en kondensator og en modstand, hvilket gør det enkelt, men alligevel meget effektivt.Kondensatorer er robuste mod problemer som induktiv kobling og energispredning.I modsætning til induktorer, der lider af resistive og magnetiske tab på grund af deres fysiske makeup og materialer, opretholder kondensatorer stabil og forudsigelig ydeevne.Induktorer mister effektiviteten på grund af trådmodstand og magnetisk hysterese, problemer, som kondensatorer ikke står overfor, hvilket fører til en mere lineær og pålidelig respons under forskellige forhold.
Kapacitive filtre er især nyttige i applikationer, der kræver ensartet ydelse, såsom lydudstyr eller signalbehandlingsenheder, hvor signalintegritet er nøglen.Mens kapacitive filtre er vidt foretrukket i mange elektroniske applikationer, spiller induktive filtre stadig en nøglerolle i specifikke sammenhænge.For eksempel er der i AC-DC strømforsyningskredsløb nødvendige induktive filtre på grund af deres minimale seriemodstand, hvilket sikrer lavere effekttab og bedre effektivitet på trods af deres ineffektivitet.
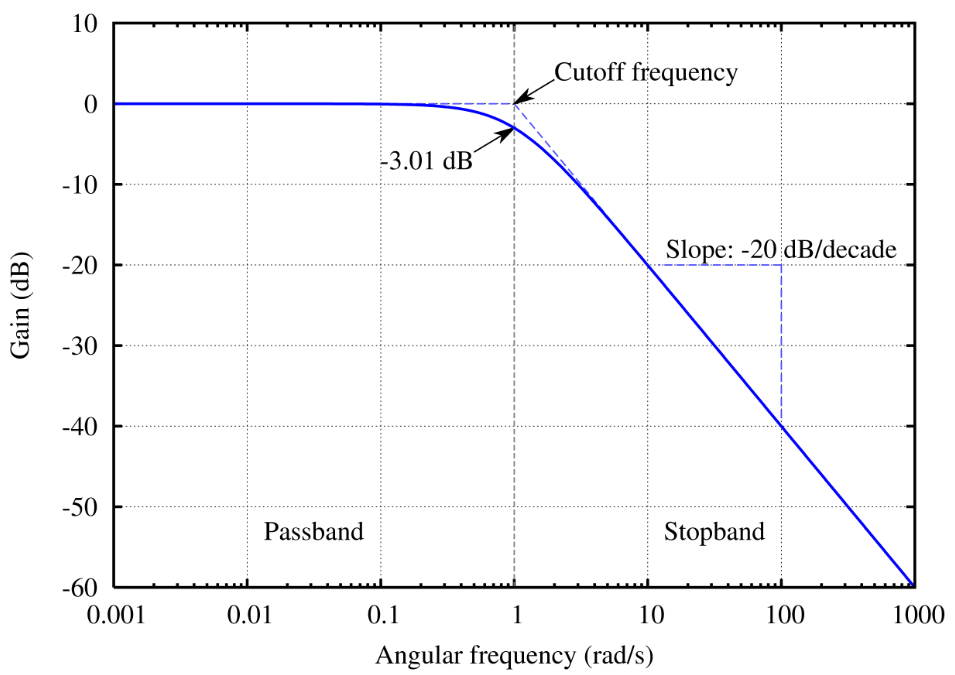
Figur 3: Cutoff -frekvens
Cutoff -frekvensens rolle i elektroniske filtre
Cutoff-frekvensen sætter sig i lavpas filterdesign, hvilket markerer det punkt, hvor filteret begynder at reducere indgangssignalet markant.Teknisk defineres det som den frekvens, hvor udgangsspændingen falder til 70,7% af sin inputværdi, svarende til en -3 dB -reduktion i den logaritmiske skala, hvilket indikerer halvering af strømmen.Nøgleparametre som resistens og kapacitans bestemmer denne frekvens i kapacitive-resistive lavpasfiltre.
For at beregne cutoff -frekvensen indstiller du den kapacitive reaktans, der er lig med modstanden.Formlen er 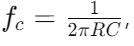 , hvor er
, hvor er 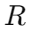 modstand,
modstand, er kapacitans og
er kapacitans og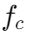 er cutoff -frekvensen.Denne beregning antager ideelle forhold, men den virkelige verden udfører ofte på grund af faktorer som ændringer i belastningsmodstand og den ikke-ideelle karakter af komponenter, herunder parasitiske kapacitanser og induktanser, der ikke overvejes i det indledende design.
er cutoff -frekvensen.Denne beregning antager ideelle forhold, men den virkelige verden udfører ofte på grund af faktorer som ændringer i belastningsmodstand og den ikke-ideelle karakter af komponenter, herunder parasitiske kapacitanser og induktanser, der ikke overvejes i det indledende design.
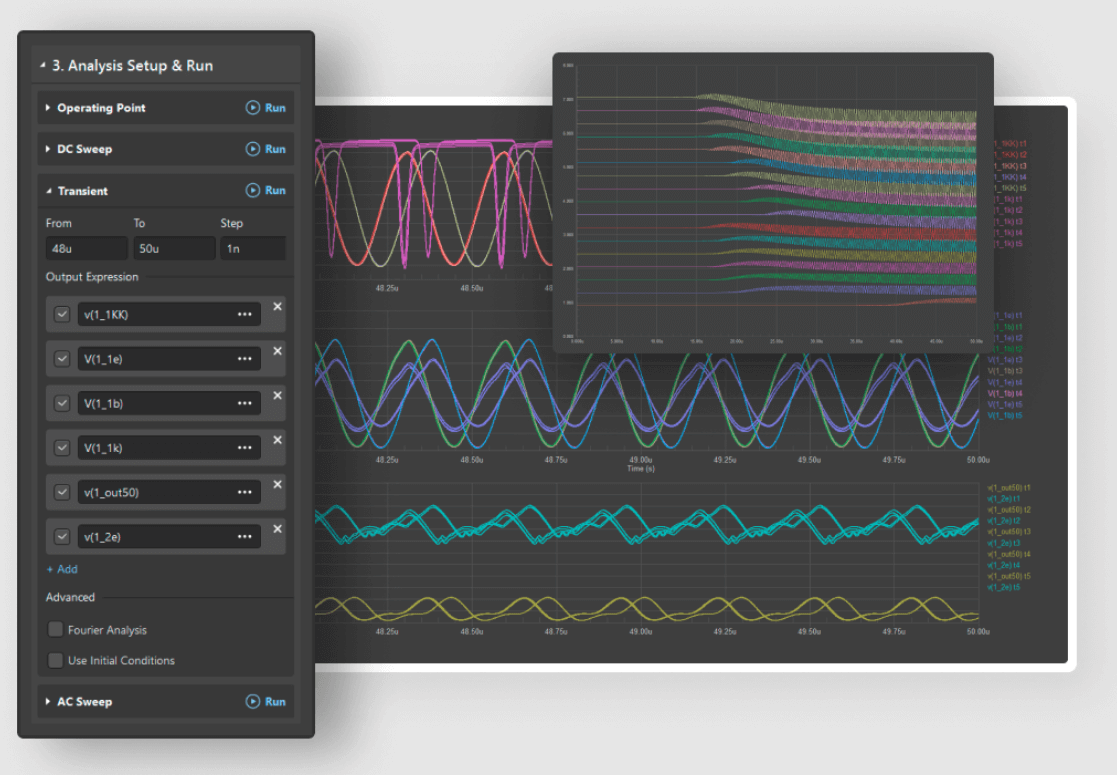
Figur 4: Krydderimuleringer
For at tackle disse uoverensstemmelser bruger designere krydderi -simuleringer til at modellere filtre under realistiske forhold.Disse simuleringer tillader dynamisk justering af parametre at tilpasse sig de ønskede resultater.Det er også vigtigt at forstå, hvordan cutoff -frekvensen fungerer i sammenhæng med et kredsløb.Faktorer som temperatur og fugtighed kan påvirke komponentegenskaber og flytte den faktiske afskæringsfrekvens.
Praktiske anvendelser af lavpasfiltre
Lavpasfiltre er nødvendige for at forbedre ydelsen og pålideligheden af elektroniske systemer, især i miljøer med betydelig interferens og støj.I strømforsyninger til elektroniske enheder sikrer disse filtre stabiliteten og renheden af DC-output ved at eliminere højfrekvent støj.Denne støj kan stamme fra forskellige kilder, såsom kapacitiv og induktiv kobling fra nærliggende kredsløb, og kan forstyrre enhedens funktionalitet.En enkel, men alligevel effektiv løsning er at placere en kondensator på tværs af belastningen og danne et lavpasfilter, der dirigerer højfrekvente forstyrrelser væk fra usikre komponenter.Denne metode er især nyttig på tæt befolkede kredsløbskort, hvor adskillige elektroniske komponenter er i nærheden, hvilket skaber udfordringer til at opretholde signalintegritet.
Valget af filter - hvad enten det er at bruge kondensatorer, induktorer eller en kombination - afhænger af kredsløbets specifikke behov, herunder støjtypen og følsomheden af nedstrøms komponenter.For eksempel kræver lydelektronik ofte komplekse filterdesign for at bevare signalkvaliteten og sikre en uforvrænget output.Lavpasfiltre bruges ikke kun til støjreduktion, men spiller også en betydelig rolle i analog-til-digital konvertering.De begrænser indgangssignalets båndbredde til Nyquist -frekvensen for at forhindre aliasering, hvilket kan forringe konverteringsnøjagtigheden.I trådløs kommunikation blokerer disse filtre højfrekvente signaler uden for det ønskede frekvensbånd, hvilket forhindrer interferens og krydstale mellem kommunikationskanaler.
Lavpas filtre bruges i vid udstrækning ud over traditionelle elektroniske kredsløb, hvilket påvirker forskellige felter fra digitale medier til sundhedsydelser.
Raffinering af visuelle medier gennem billedbehandling
I digital billedbehandling forbedrer lavpasfiltre kvaliteten af visuelle medier ved at udjævne og sløres billeder.Denne teknik reducerer pixelstøj og højfrekvente artefakter, der forringer billedkvaliteten.Det er især værdifuldt inden for digital fotografering og videoproduktion, hvor afbalancering af billedskarphed med støjreduktion i høj grad påvirker visuel appel og klarhed.I realtidsapplikationer som videostreaming eller augmented reality hjælper lavpasfiltre med at opretholde høj visuel kvalitet på trods af live datatransmissionsudfordringer.
At sikre klarhed i telekommunikationssystemer
I telekommunikation administrerer lavpasfiltre signalintegritet ved at begrænse båndbredden af transmitterede signaler for at forhindre interferens med høj frekvens, der kan ødelægge data og forstyrre kommunikation.At sikre kvaliteten af signalet på tværs af udvidede afstande er en betydelig anvendelse i både analoge og digitale kommunikationssystemer.Ved at bruge lavpasfiltre reduceres fejl, og den samlede pålidelighed af kommunikationskanaler forbedres.
Forbedring af diagnostisk nøjagtighed i biomedicinske anvendelser
I det biomedicinske felt forbedrer lavpasfiltre læsbarheden og pålideligheden af fysiologiske signaloptagelser, såsom elektroencefalogrammer (EEG) og elektrokardiogrammer (EKG).Disse enheder er følsomme over for højfrekvent støj, der kan skjule kritiske data, hvilket gør nøjagtig diagnose vanskelig.Ved at integrere lavpasfiltre opnår læger klarere signaler, forbedrer diagnostisk proces og letter mere effektive behandlingsplaner.Denne applikation fremhæver filterets betydning i sundhedsydelser, hvor klarheden i fysiologiske signaler direkte påvirker patientresultater.
Optimering af lydsystemer med lavpasfiltre
Lavpasfiltre er også et alsidigt værktøj for lydingeniører, der tillader manipulation af lydbilleder at opnå forskellige kunstneriske og tekniske effekter.Her er innovative måder, disse filtre kan anvendes i lydindstillinger:
Forbedring af rumlig dybde i blandinger
Lydingeniører bruger lavpasfiltre til at tilføje dybde og dimension til lydspor.Ved at reducere højere frekvenser kan lyde gøres til at virke mere fjernt.Denne effekt er især nyttig i komplekse blandinger, hvor det at skelne mellem forgrunds- og baggrundselementer forbedrer den samlede klarhed og den rumlige opfattelse.Denne teknik efterligner auditive oplevelser i den virkelige verden, hvor afstand naturligt filtrerer højere frekvenser, hvilket får lyde til at virke længere væk.
Oprydning af lydspor
I både studie- og live lydmiljøer er filtre med lav passager nyttige til at eliminere højfrekvent støj eller interferens.Almindelige problemer som sus, elektrisk brummen eller alt for skarpe lyde fra digitale kilder kan minimeres effektivt.Ved at skære ud disse uønskede frekvenser bliver den ønskede lyd renere, forbedrer produktionens samlede tro og sikrer et poleret slutprodukt.
Afbalanceringsfrekvenser i komplekse blandinger
Lavpasfiltre er nøglen til styring af frekvensmaskering, en fælles udfordring i tæt musikalske arrangementer, hvor flere lyde konkurrerer inden for det samme frekvensområde.Ved selektivt at dæmpe højere frekvenser på visse spor, kan lydingeniører forhindre, at imperative elementer overskygges, opretholder et harmonisk og afbalanceret akustisk miljø i blandingen.
Oprettelse af soniske variationer
Lavpas filtre giver lydfagfolk mulighed for at skabe variationer af den samme lyd inden for en sammensætning og berige det auditive landskab.Dette kan være særligt effektivt til at tilføje dynamiske skift inden for et spor, ændre klang og tilstedeværelse af lyde, der passer til forskellige sektioner eller følelsesmæssige toner, og derved forbedre den musikalske fortælling uden at introducere nye elementer.
Raffinering af lyddefinition i tætte blandinger
I komplekse lydblandinger forbedrer lavpasfiltre definitionen og fokus for bestemte lyde.Ved at reducere højere frekvenser bliver den resterende lyd klarere, hvilket gør det muligt for lyttere bedre at værdsætte subtile detaljer og tilsigtede nuancer.
Optimering af effekter busser
Lavpasfiltre er også nødvendige for at styre effektbusser, såsom reverb eller forsinkelse afsendelser.Påføring af disse filtre kontrollerer overdreven høje frekvenser, der ellers kan dominere virkningerne, hvilket sikrer, at de tilføjer til blandingen uden at blive påtrængende.Denne omhyggelige kontrol opretholder den samlede balance og æstetik af blandingen, hvilket gør det muligt for virkningerne at forbedre snarere end at overmanne de primære elementer.
Afklaring af konkurrerende lyde
Håndtering af frekvensmaskering, hvor flere lyde konkurrerer om det samme auditive rum, er en almindelig blandingsudfordring.Lavpas filtre er uvurderlige her, da de dæmper de høje frekvenser af nogle spor for at forhindre dem i at overskygge andre.Dette hjælper med at opretholde en afbalanceret blanding, hvor hvert instrument eller vokal kan værdsættes tydeligt.
Udforskning af de forskellige former for lavpasfiltre
Lavpas filterkredsløb er nøglen i forskellige elektroniske systemer, designet til at lade lavfrekvente signaler passere, mens de reducerer højere frekvenser.Valget af filtertype afhænger af specifikke applikationsbehov og ønskede signalegenskaber, hvor hver type tilbyder unikke fordele.
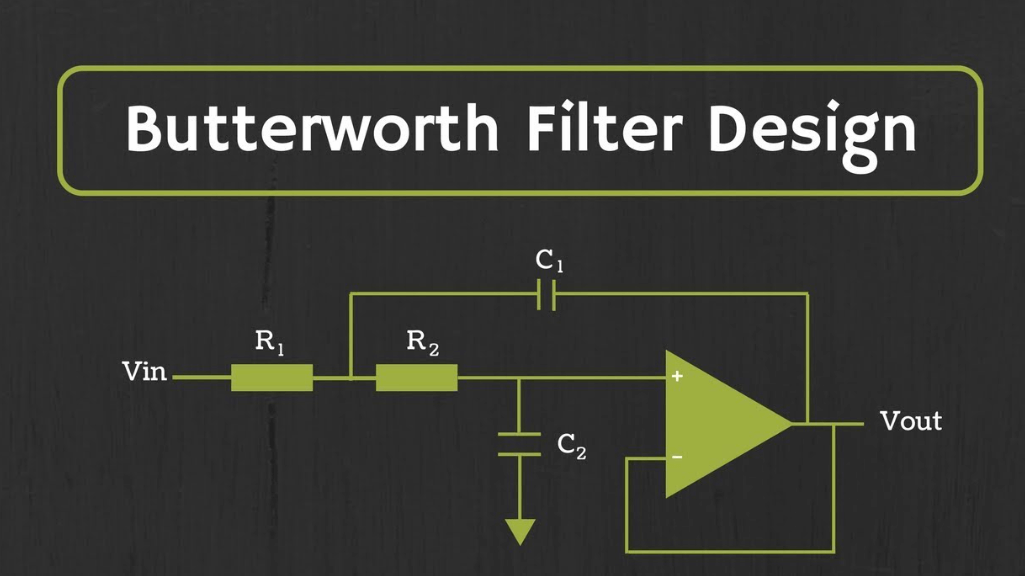
Figur 5: Butterworth -filtre
Butterworth -filtre er kendt for deres flade passbåndsrespons, hvilket betyder, at de ikke introducerer nogen krusning i passbåndet.Dette gør dem ideelle til lydbehandling og andre applikationer, hvor opretholdelse af signalintegritet inden for passbåndet er et must.Deres design sikrer en lineær respons, der minimerer lydsignalforvrængning, hvilket er vigtigt for lydsystemer med høj tro og præcise måleinstrumenter.
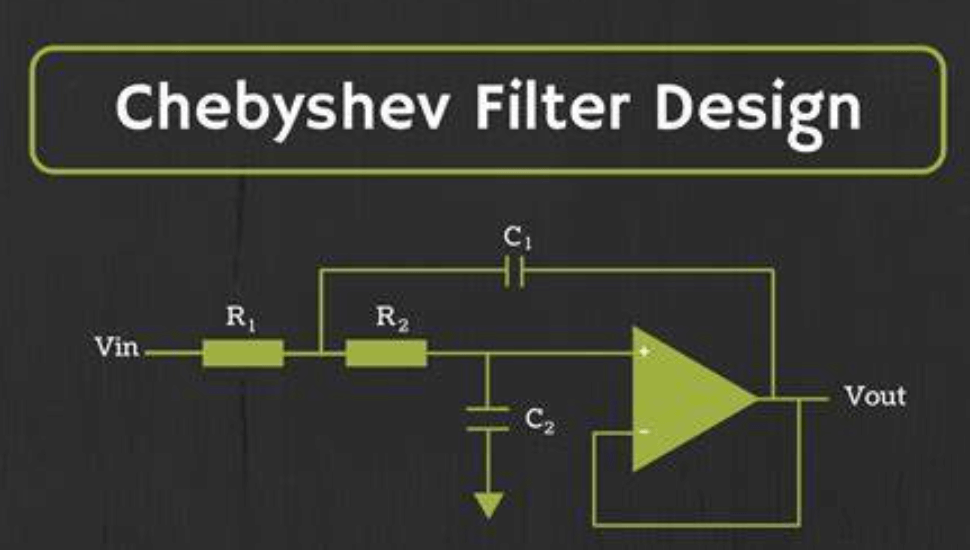
Figur 6: Chebyshev -filtre
Chebyshev -filtre opnår en skarpere rulle end Butterworth -filtre, hvilket giver bedre adskillelse mellem passbåndet og stopbåndet.Dette gøres på bekostning af en eller anden krusning i passaget, en afvejning, der er acceptabel i scenarier, hvor en stejl cutoff er mere usikker.Disse filtre bruges ofte i kommunikationssystemer, hvor præcis båndbreddebegrænsning er mere dominerende end minimal passbånd.
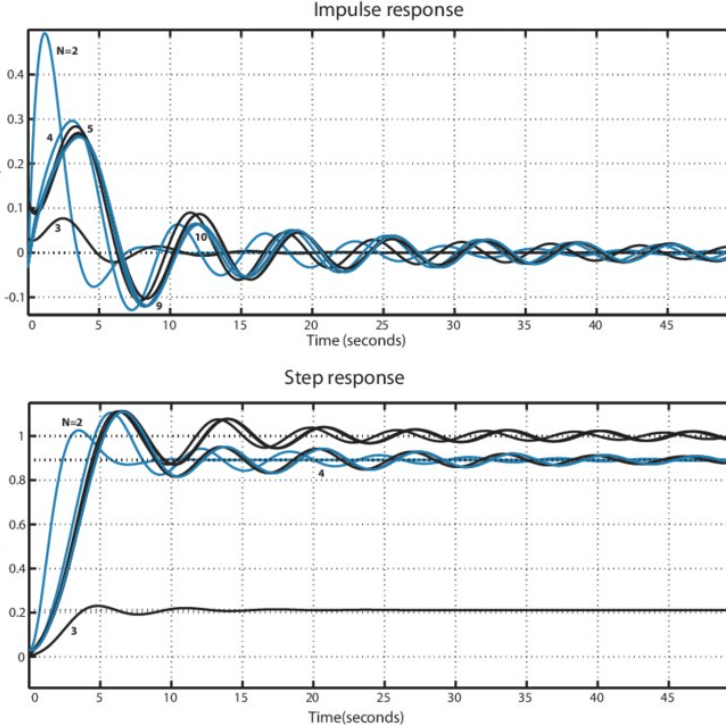
Figur 7: Elliptiske filtre
Elliptiske filtre (også kendt som Cauer Filtre) tilbyder den stejleste roll-off, hvilket giver mulighed for en minimal overgang fra passbånd til StopBand.Dette gør dem effektive i applikationer, hvor optælling af rum og komponent er begrænsede, såsom bærbare og miniaturiserede elektroniske enheder.Den skarpe overgang er fordelagtig i tætpakket frekvensspektre, hvor minimering af tilstødende kanalinterferens er betydelig.
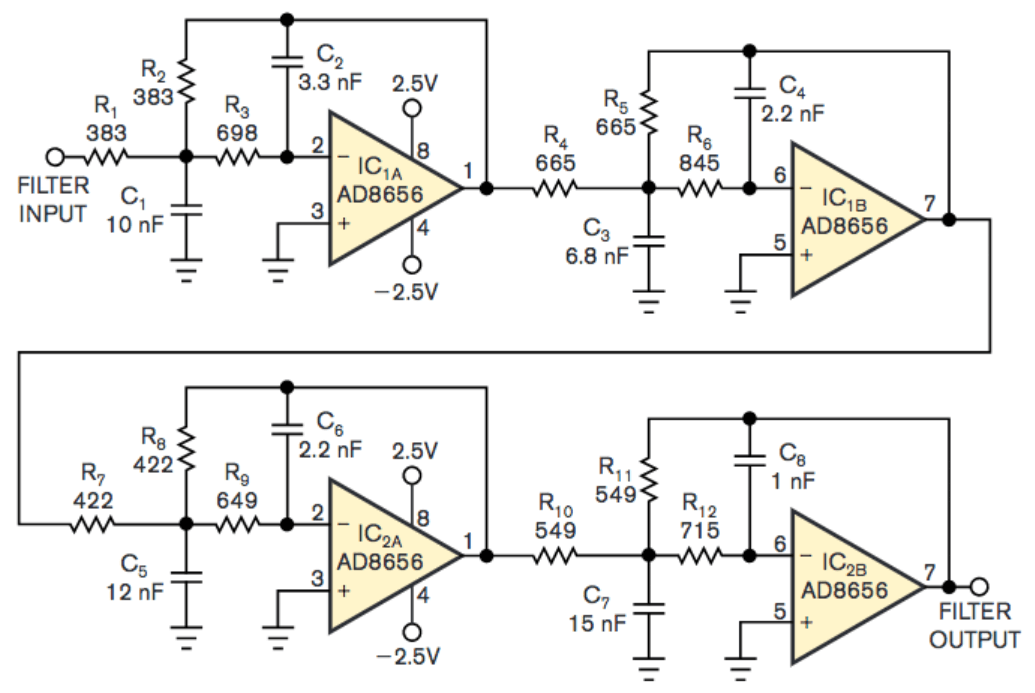
Figur 8: Bessel filtre
Mens Bessel filtre, mens de tilbyder en blødere roll-off, udmærker sig i at bevare fasen og formen af indgangssignalet i hele passbåndet.Dette er dynamisk i applikationer som Pulse Communications, Instrumentation og Audio Crossovers, hvor opretholdelse af de tidsmæssige egenskaber ved det originale signal sikrer nøjagtighed og tro.
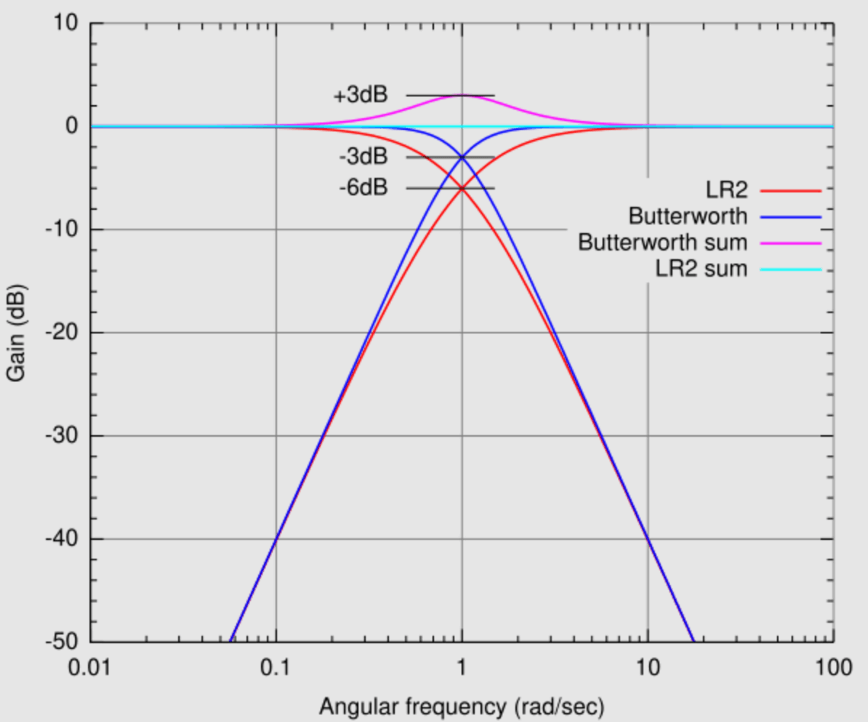
Figur 9: Linkwitz-Riley-filter
Med en stejl 24 dB/oktavhældning er dette filter nøglen i applikationer, hvor nøjagtig frekvensafdeling er påkrævet, såsom flervejshøjttalersystemer.I en tovejs højttaleropsætning deler LinkWitz-Riley-filteret frekvenser nøjagtigt og sender høje frekvenser til tweeteren og lave frekvenser til wooferen.Dette sikrer en jævn frekvensrespons med minimale faseproblemer, som er dynamisk til at opretholde lydintegritet i miljøer, hvor lydkvaliteten er utrygt, som professionelle optagestudier eller lydsystemer med høj tro.
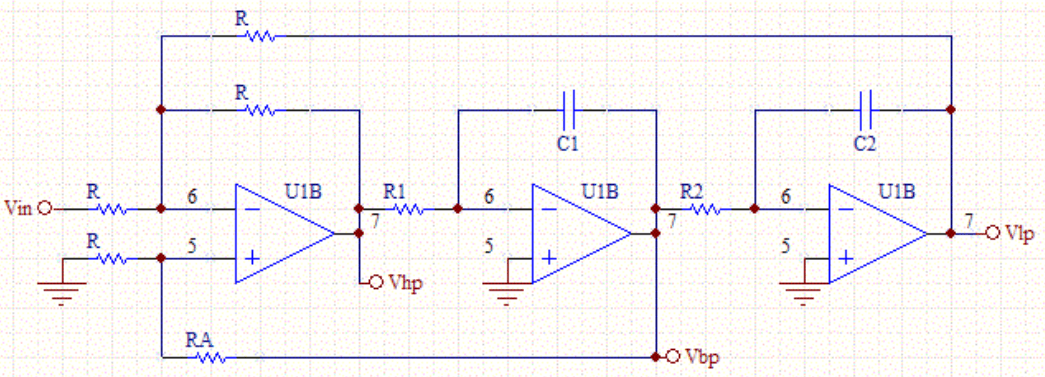
Figur 10: Tilstandsvariabelfilter
Det statslige variable filter er bemærkelsesværdigt for dets alsidighed og anvendelighed ved lydsyntese.I modsætning til traditionelle filtre giver det samtidig lavpas, højpas og båndpasudgange.Denne multi-mode-funktionalitet giver mulighed for detaljeret kontrol over lydens timbrale kvaliteter i realtid, hvilket gør det nødvendigt til at skabe elektronisk musik.Evnen til at skifte glat mellem forskellige filtertyper hjælper producenterne med at skabe komplicerede soniske strukturer og dynamiske ændringer i deres musik.I synthesizere kan dette filter modulere lyde fra dybe basser til sprøde højder, hvilket gør det nødvendigt for lyddesignere.
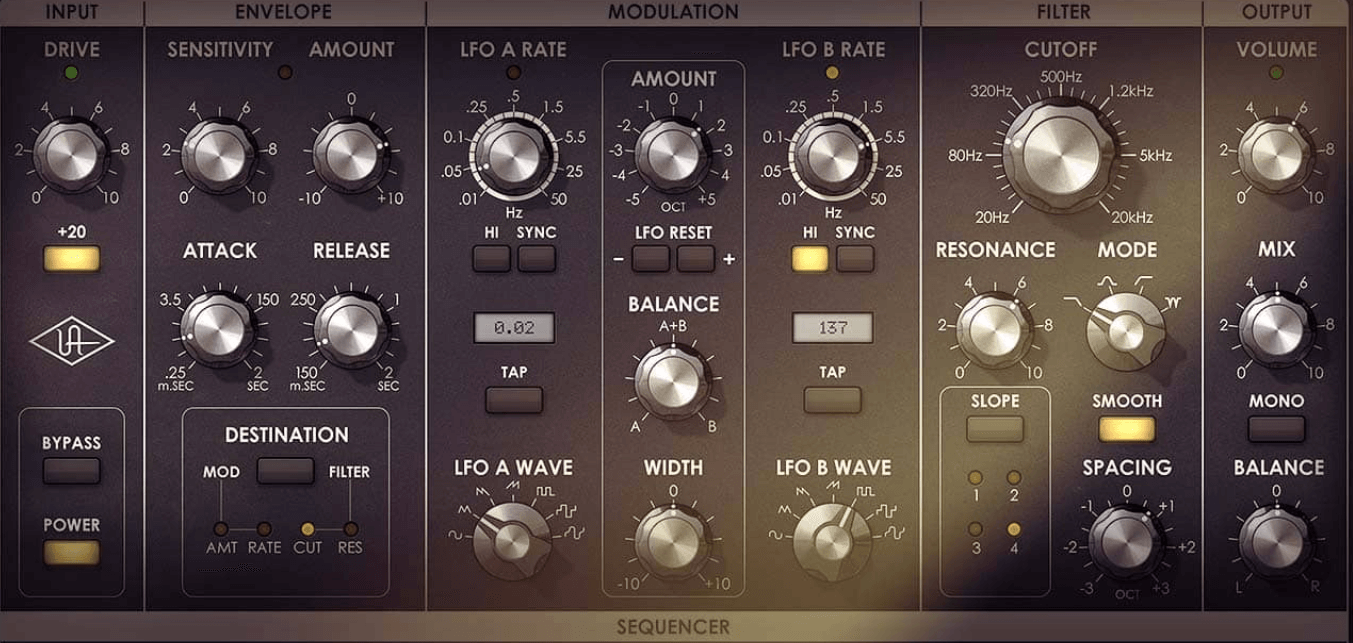
Figur 11: Moog -filter
Kendt for sin varme, rige lyd og karakteristiske resonansstyring har den i høj grad påvirket forskellige musikgenrer, især elektronisk musik.Moog-lavpasfilteret forbedrer synthesizer-lyde fra dybe basser til glatte ledninger.Dens resonansfunktion fremhæver frekvenser ved cutoff -punktet og skaber en top, der tilføjer harmonisk kompleksitet.Dette gør Moog -filteret til en favorit blandt musikere og producenter, der søger at tilføje dybde, varme og en analog fornemmelse af deres spor, der cementerer dets vedvarende arv i musikproduktionen.
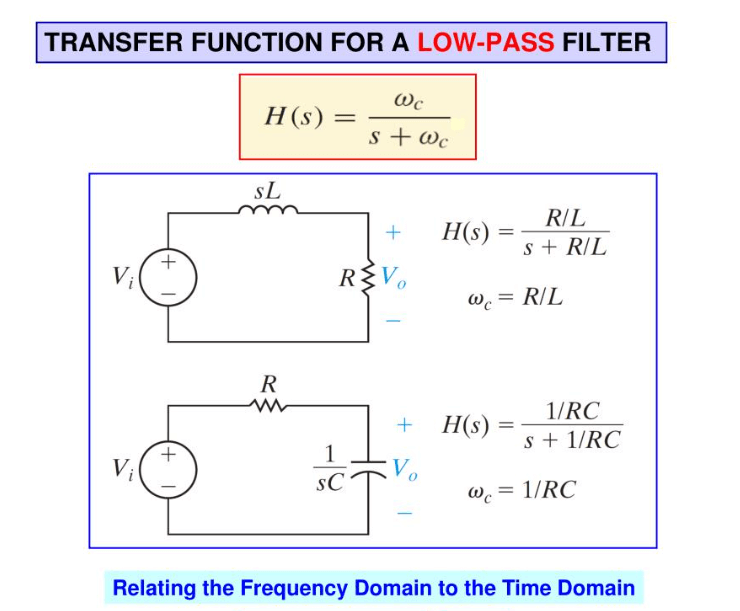
Figur 12: Overførselsfunktion i lavpas filterdesign
Analyse af overførselsfunktionen af lavpasfiltre
Oprettelse af effektive filtreringsløsninger kræver en omfattende viden om et lavpasfilters overførselsfunktion.Dette matematiske udtryk viser, hvordan amplituden og fasen af et udgangssignal varierer i forhold til indgangssignalet på tværs af forskellige frekvenser.Overførselsfunktionen er afledt af filterets komponenter - modstand (R), kapacitans (C) og undertiden induktans (L) - og beskriver filterets frekvensrespons.
Overførselsfunktionen, betegnet Hvor SSS er den komplekse frekvensvariabel, fanger filterets dynamik.For et simpelt RC-lavpasfilter er overførselsfunktionen:
Hvor SSS er den komplekse frekvensvariabel, fanger filterets dynamik.For et simpelt RC-lavpasfilter er overførselsfunktionen: 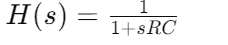 Denne ligning viser, hvordan filteret dæmper højfrekvente signaler, mens de tillader lave frekvenser at passere med mindre dæmpning.RC -produktet, kendt som tidskonstanten, påvirker direkte cutoff -frekvensen, det punkt, hvor filteret begynder at dæmpe højere frekvenser markant.
Denne ligning viser, hvordan filteret dæmper højfrekvente signaler, mens de tillader lave frekvenser at passere med mindre dæmpning.RC -produktet, kendt som tidskonstanten, påvirker direkte cutoff -frekvensen, det punkt, hvor filteret begynder at dæmpe højere frekvenser markant.
I lydbehandling hjælper overførselsfunktionen med at designe systemer, der kontrollerer frekvensdæmpning for at opretholde lydkvalitet og reducere støj.I telekommunikation giver det ingeniører mulighed for at oprette kredsløb, der filtrerer højfrekvent støj, hvilket sikrer klar signaloverførsel.
Overførselsfunktionen er et risikabelt værktøj til at forudsige og analysere et filters opførsel under forskellige forhold.Ved at justere parametre inden for overførselsfunktionen kan designere se, hvordan ændringer i komponentværdier påvirker filterets ydelse.Dette er især nyttigt i iterative designprocesser, hvor flere prototyper kan testes for at opnå optimale resultater.
Mastering af kontrollerne med lavpasfiltre
Lavpasfiltre spiller en kerne rolle i udformningen af lydsignaler, hvilket tillader præcis kontrol over hvilke frekvenser fremhæves eller reduceres.Dette afsnit undersøger de grundlæggende principper og funktioner i lavpasfiltre, hvilket understreger deres krævede rolle i lydbehandling.
Hældning og resonans
Hældningen af et lavpasfilter indikerer, hvor hurtigt frekvenser over afskæringen reduceres, hvilket påvirker filterets output.En stejlere hældning betyder et skarpere fald i høje frekvenser, hvilket hjælper med at isolere lavere frekvenser mere effektivt.Derudover kan resonanskontrollen øge frekvenserne ved afskæringen, tilføje en unik lydkvalitet og forbedre specifikke toner.Denne kontrol giver producenterne mulighed for at tilføje vibration og definere musikens karakter.
Q Faktor
Q-faktoren eller kvalitetsfaktoren måler båndbredden omkring afskæringsfrekvensen, hvor resonans er mærkbar.En høj Q -faktor understreger et snævert frekvensområde, der bringer mere fokus til dette område.En lav Q -faktor spreder resonansen over et bredere interval og udjævner frekvensresponsen.Denne parameter er fokal for lydingeniører, der sigter mod at tilpasse lyde til at imødekomme specifikke kunstneriske eller tekniske behov.
Modulation gennem konvolut tilhængere
Moduleringskontroller, som en konvolutfølger, forbedrer den dynamiske respons fra lavpasfiltre ved at variere afskæringsfrekvensen i realtid i henhold til indgangssignalets amplitude.Denne funktion giver filteret mulighed for at tilpasse sig et musikalsk stykke dynamik og tilføje rytmisk og strukturel kompleksitet.Ekstern moduleringskontrol udvider kreative muligheder i lyddesign, hvilket gør det særlig værdifuldt inden for elektronisk musik, hvor dynamiske strukturelle ændringer markant kan påvirke sporets fornemmelse og progression
Konklusion
Udforskningen af lavpasfiltre på tværs af flere domæner understreger deres uundværlige rolle i nutidig teknologi.Fra raffinering af lydblandinger i musikproduktion til forbedring af pålideligheden af elektroniske kommunikationssystemer, lavpasfiltre tilpasser sig til en bred vifte af udfordringer, hvilket sikrer optimal ydelse og tro.Den detaljerede undersøgelse af forskellige filtertyper, såsom Butterworth, Chebyshev og Moog -filtre, afslører deres unikke fordele i specifikke applikationer, der fremhæver nødvendigheden af skræddersyet filterdesign for at imødekomme nøjagtige operationelle krav.
Integrationen af avancerede simuleringsværktøjer og dyb overvejelse af cutoff-frekvensdynamik forbedrer yderligere evnen til at forudsige og finjustere filteradfærd under forhold i den virkelige verden.Efterhånden som teknologien skrider frem, vil den kontinuerlige udvikling af lavpas filterdesign utvivlsomt spille en betydelig rolle i at fremme elektronisk teknik og lydproduktion og udskære en vej til innovative løsninger, der adresserer både aktuelle og fremtidige udfordringer i signalbehandling.
Ofte stillede spørgsmål [FAQ]
1. Hvad er et højpas og lavpas filter?
Et højpasfilter gør det muligt for frekvenser over en bestemt cutoff-frekvens at passere gennem og dæmpe frekvenser under denne cutoff.Omvendt tillader et lavpasfilter frekvenser under en specifik cutoff-frekvens at passere og dæmpe dem over det.
2. Hvad er fordelene ved et lavpasfilter?
Støjreduktion: De reducerer effektivt højfrekvent støj, hvilket gør dem nyttige i lyd- og elektronisk signalbehandling.
Signaludjævning: Lavpasfiltre bruges til at glatte data ved gennemsnit af hurtige udsving, nyttige i dataanalyse og elektroniske kredsløbsapplikationer.
Stabilitet: De hjælper med at stabilisere kontrolsystemer ved at filtrere højfrekvente svingninger.
3. Hvad er formålet med lavpasfiltre i billedbehandling?
I billedbehandling tjener et lavpasfilter til at sløre billeder, hvilket kan reducere støj og detaljer.Denne sløringseffekt udjævner hurtige intensitetsændringer, hvilket hjælper med billedforbedring og analyse, især til at fjerne småskala detaljer for at fokusere på større strukturer.
4. Hvordan fungerer aktive lavpasfiltre?
Aktive lavpasfiltre bruger aktive komponenter som forstærkere sammen med modstande og kondensatorer til at filtrere signaler.Forstærkeren kompenserer for signaltabet på grund af filtrering og opretholder således signalstyrken.Denne opsætning giver filteret mulighed for at håndtere lavfrekvente signaler effektivt uden signifikant nedbrydning og let at blive integreret i forskellige elektroniske kredsløb på grund af dets aktive karakter.
5. Hvad er ulemperne ved lavpasfilter?
Tab af betydelige detaljer: Ved at dæmpe høje frekvenser kan nogle betydelige detaljer i signaler, såsom skarpe overgange eller specifikke signalfunktioner, gå tabt.
Faseskift: De kan introducere et faseskift i de filtrerede signaler, som kan være problematiske i applikationer, der kræver nøjagtig fasejustering.
Designkompleksitet: Design af et effektivt lavpasfilter, der nøjagtigt afbalancerer cutoff-frekvens og signalintegritet, kan være kompleks, især i aktive filtre, hvor komponentvalg og konfigurationseffektydelse.
Om os
ALLELCO LIMITED
Læs mere
Hurtig forespørgsel
Send en forespørgsel, vi svarer med det samme.
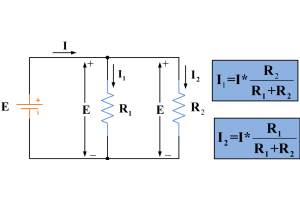
Aktuelle dividerkredsløb og effektiv brug af dividerformlen
på 2024-06-14
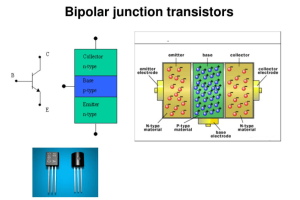
En komplet guide til forståelse af bipolære forbindelsestransistorer (BJT)
på 2024-06-13
Populære indlæg
-
Hvad er GND i kredsløbet?
på 1970-01-01 2946
-

RJ-45 Connector Guide: RJ-45 Stikfarvekoder, ledningsordninger, R-J45-applikationer, RJ-45 datablad
på 1970-01-01 2502
-

Fiberstikstyper: SC vs LC og LC vs MTP
på 1970-01-01 2091
-
Forståelse af strømforsyningsspændinger i elektronik VCC, VDD, VEE, VSS og GND
på 0400-11-09 1898
-

Sammenligning mellem DB9 og RS232
på 1970-01-01 1765
-

Hvad er et LR44 -batteri?
Elektricitet, den allestedsnærværende kraft, roligt gennemsyrer alle aspekter af vores daglige liv, fra trivielle gadgets til livstruende medicinsk udstyr, det spiller en stille rolle.Imidlertid er det ingen let opgave at gribe ind i denne energi, især hvordan man opbevarer og effektivt udsender den.Det er på denne baggrund, at denne artikel vil fokusere på en type møntcellebatteri, der kan ...på 1970-01-01 1714
-

Forståelse af de grundlæggende elementer: induktansresistens, og kapacitet
I den komplicerede dans inden for elektroteknik tager en trio af grundlæggende elementer centrum: induktans, modstand og kapacitans.Hver bærer unikke træk, der dikterer de dynamiske rytmer af elektroniske kredsløb.Her går vi på en rejse for at dechiffrere kompleksiteten af disse komponenter for at afsløre deres forskellige roller og praktiske anvendelser inden for det store elektriske o...på 1970-01-01 1662
-

CR2430 Batteri Comprehensive Guide: Specifikationer, applikationer og sammenligning med CR2032 -batterier
Hvad er CR2430 -batteri?Fordele ved CR2430 -batterierNormCR2430 Batteri applikationerCR2430 ækvivalentCR2430 vs CR2032Batteri CR2430 størrelseHvad man skal kigge efter, når man køber CR2430 og ækvivalenterDatablad PDFOfte stillede spørgsmål Batterier er hjertet i små elektroniske enheder.Blandt de mange tilgængelige typer spiller møntceller en afgørende rolle, der ofte findes i regnemas...på 1970-01-01 1567
-
Hvad er RF, og hvorfor bruger vi det?
Radiofrekvens (RF) -teknologi er en vigtig del af moderne trådløs kommunikation, der muliggør datatransmission over lange afstande uden fysiske forbindelser.Denne artikel dækker det grundlæggende i RF og forklarer, hvordan elektromagnetisk stråling (EMR) gør RF -kommunikation mulig.Vi vil udforske principperne for EMR, oprettelse og kontrol af RF-signaler og deres omfattende anvendelser.Art...på 1970-01-01 1550
-

CR2450 vs CR2032: Kan batteriet bruges i stedet?
Lithium -manganbatterier har nogle ligheder med andre lithiumbatterier.Høj energitæthed og lang levetid er de egenskaber, de har til fælles.Denne form for batteri har vundet tillid og fordel for mange forbrugere på grund af dens unikke sikkerhed.Dyre tech -gadgets?Små apparater i vores hjem?Se dig omkring, så ser du dem overalt.Blandt disse mange lithium-manganske batterier er CR2450-batteri...på 1970-01-01 1519

















































